Question: X Excel Tutorial_Product Function,xIsx . Last Modified: Just now v Search Jesse Bob Davies JB X File Home Insert Draw Page Layout Formulas Data Review
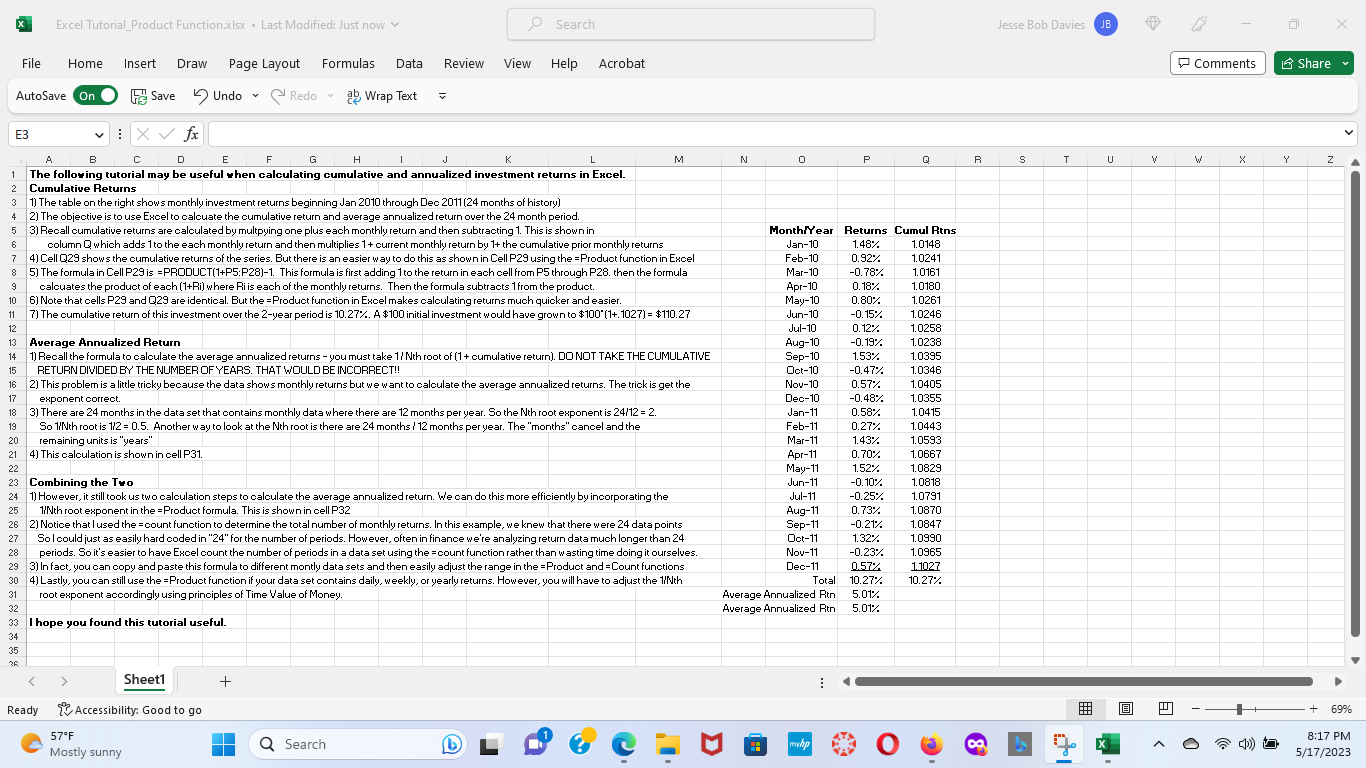
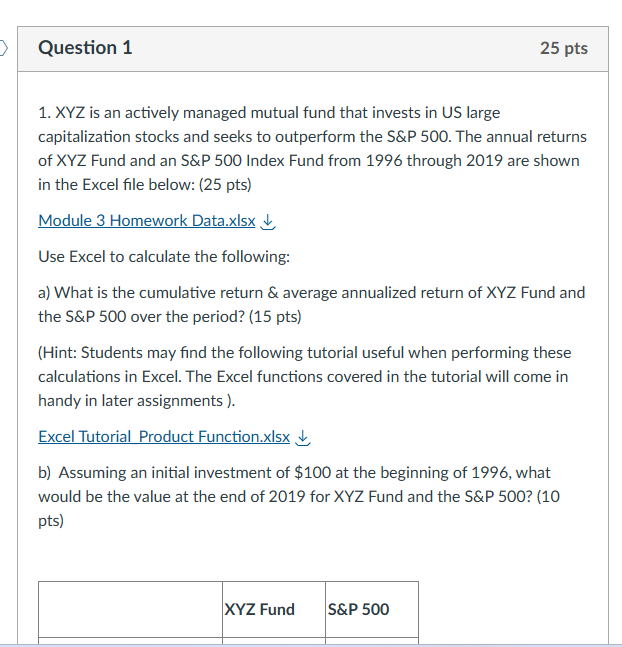
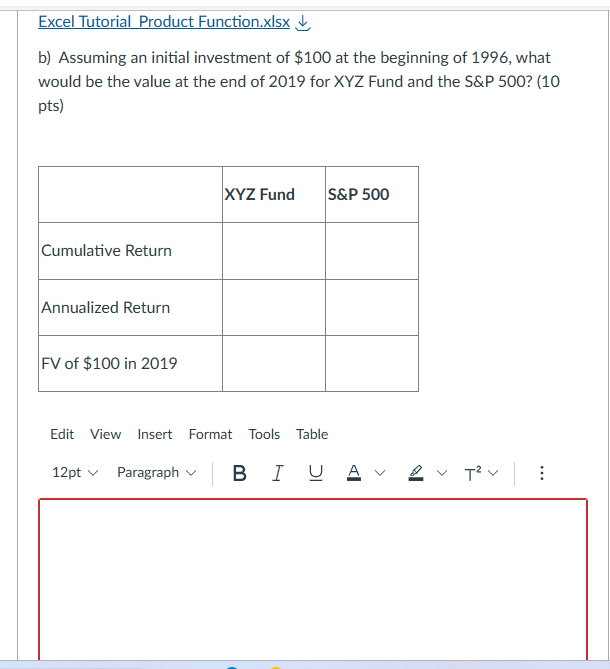
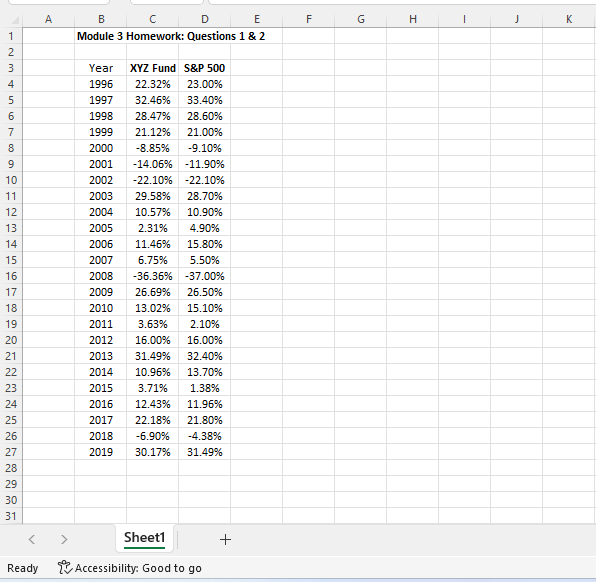
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


