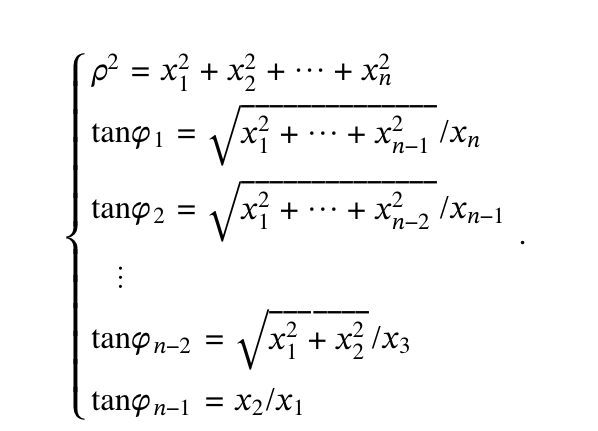
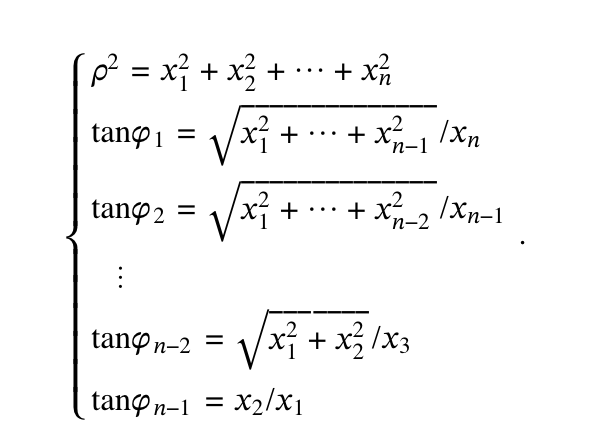
X1 = p sing 1 sing 2 . . . sinon-2 cosOn-1 X2 = p sing , sing 2 . . . sinon-2 sinon-1 X3 = p sing 1 sing 2 . . . sinon-3 cosOn-2 X4 = p sing 1 sing2 . . . sinon-4 cosOn-3 . . . Xn = p cosQ1 To be more explicit, in equation (10) above we take Xk = p sin $ 1 sin 92 . . . sin On-k cos On-k+1 for k = 3, ... , n. Note that when n = 3, the relations in (10) become X1 = p sing 1 cosQ 2 X2 = p sing 1 sing 2 . X3 = p cosQ1\fa. Calculate x, + x3 in terms of the hyperspherical coordinates p, Q1, ... , Pn-2. b. Assuming the inequalities in (11), use part (a) to show that tan On-2 =Vx, + x21X3