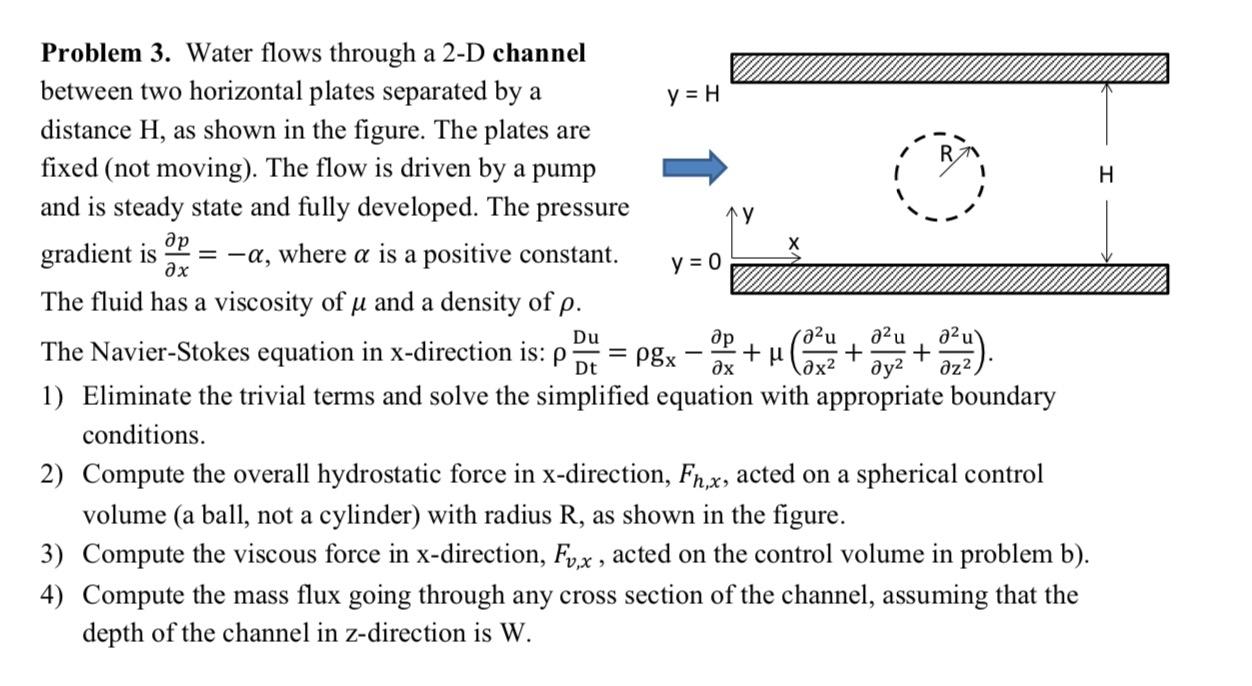
y = H H a y = 0 a2u Problem 3. Water flows through a 2-D channel between two horizontal plates separated by a distance H, as shown in the figure. The plates are fixed (not moving). The flow is driven by a pump and is steady state and fully developed. The pressure gradient is = -a, where a is a positive constant. The fluid has a viscosity of u and a density of p. a2u 22u The Navier-Stokes equation in x-direction is: op+uco + + + (ax 1) Eliminate the trivial terms and solve the simplified equation with appropriate boundary conditions. 2) Compute the overall hydrostatic force in x-direction, Fn,x, acted on a spherical control volume (a ball, not a cylinder) with radius R, as shown in the figure. 3) Compute the viscous force in x-direction, Fv,x , acted on the control volume in problem b). 4) Compute the mass flux going through any cross section of the channel, assuming that the depth of the channel in z-direction is W. Du p Dt = P8x ? z2