Question: You are given a directed graph G = (V, E) with positive edge weights w : V R>0. You start with a car at a

You are given a directed graph G = (V, E) with positive edge weights w : V R>0. You start with a car at a specified vertex s V and you are trying to reach the destination t V. The weight w(u, v) indicates how long it takes your car travel from vertex u to v. The goal is to compute the shortest time it takes to travel from s to t, but with a twist. The twist is that your car is equipped with a single turbo charge. You can activate the turbo charge at any node in your trip, and this has an effect of reducing the travel time along the next edge to a third of the corresponding weight. Thus, it takes w(u,v)/3 to travel from vertex u to vertex v if you decide to activate the turbo charge at the time you visit u. You can activate the turbo charge at most once during the entire trip. Design an efficient algorithm for computing the shortest time it takes you to travel from s to t. 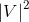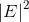Inefficient solutions with running times with quadratic terms, e.g., You are given a directed graph G = (V, E) with positive or edge weights w : V R>0. You start with a car at , may lose points.

Hint: you might want to define a different graph based on the input graph.

(a) Design a correct algorithm for this problem. Describe your algorithm in plain English and briefly argue correctness. (b) Describe your algorithm in pseudocode.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

1. (20 pts) You are given a directed graph G = (V, E) with positive edge weights w: V R>o. You start with a car at a specified vertex s EV and you are trying to reach the destination t EV. The weight...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

(iii) Now express your decision rule instead using only the quantities p(Ck), p(Cj ), p(x|Ck), p(x|Cj ), and relate it to the diagram above. [2 marks] (iv) If the classifier decision rule assigns...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Suppose there is a strongly connected directed graph G = (V, E) with positive edge weights. It contains a specific edge eo ? E. Modifying Dijkstra's algorithm below, find the shortest paths between...

Shortest path: (a) You are given a strongly connected directed graph G = (V, E) with positive edge weights along with a particular node V . Describe an O((|V | + |E|) lg |V |) time algorithm for...

We are given a directed graph G = ( V , E ) with positive weight function: w : E - > R > 0 , and two vertices s , t in V . Suppose we have already computed the d and \ pi array using the Dijkastra s...

Given a directed graph G= (V; E) with nonnegative edge weights and the shortest path distances d(s; u) from a source vertex s to all other vertices in G. However, you are not given the shortest path...

Eukaryotic cells must sort their chromosomes during mitosis so each daughter cell receives the correct number of chromosomes. Why don't bacteria need to sort their chromosomes?

What is community identity? Discuss its characteristics.

Question 2 4 3 pts Luis is managing a portfolio for a group of clients. He invests in a set of high - risk cryptocurrency startups expecting them to outperform the market simply because of their risk...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

What are Decision Trees?

What is meant by the Term Glass Ceiling?

What Interface is used to develop Data Mining Structures in SQL Server Analytical Databases?