Question: You are given a linear programming problem. Maximize P = 3.5x + 3y subject to 5x + 3y 30 2x + 3y 21 XS

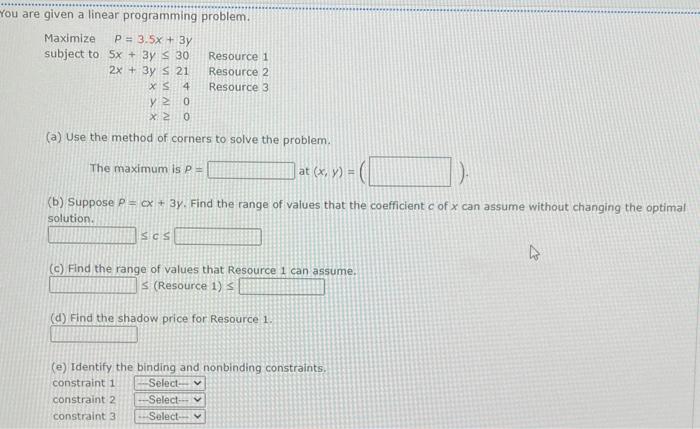
You are given a linear programming problem. Maximize P = 3.5x + 3y subject to 5x + 3y 30 2x + 3y 21 XS 4 Resource 1 Resource 2 Resource 3 x 0 (a) Use the method of corners to solve the problem. The maximum is P = at (x, y) = (b) Suppose P = cx + 3y. Find the range of values that the coefficient c of x can assume without changing the optimal solution. SCS (c) Find the range of values that Resource 1 can assume. $ (Resource 1) (d) Find the shadow price for Resource 1. (e) Identify the binding and nonbinding constraints. constraint 1 -Select- constraint 2 -Select-- constraint 3 Select--

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To solve the linear programming problem using the method of corners we need to find the corner points of the feasible region and evaluate the object... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

True or False. 1. If all the coefficients a1, a2, , an in the objective function p = a1x1 + a2x2 + + anxn are non-positive, then the only solution of the problem is x1 = x2 = = xn and p = 0. 2. The...

Suppose that a linear programming problem has 20 functional constraints in inequality form such that their right-hand sides (the bi) are uncertain parameters, so chance constraints with some a are...

You are given the following data for a linear programming problem where the objective is to maximize the profit from allocating three resources to two nonnegative activities. Contribution per unit =...

You are given the following forecasted information for the year 2008: Sales = $300,000,000; Operating profitability (OP) = 6%; Capital requirements (CR) = 43%; Growth (g) = 5%; and the weighted...

You are given the following forecasted information for the year 2014: sales = $300,000,000, operating profitability (OP) = 6%, capital requirements (CR) = 43%, growth (g) = 5%, and the weighted...

Assume you are given the following relationships for the Haslam Corporation: Sales/total assets ...................... 1.2 Return on assets (ROA) .............. 4% Return on equity (ROE)...

You are given the following forecasted information for the year 2016: sales = $300,000,000, operating profitability (OP) = 6%, capital requirements (CR) = 43%, growth (g) = 5%, and the weighted...

You are given the data in Problem S7.28: a) What is the break-even point in dollars for proposal X? b) What is the break-even point in dollars for proposal Y? Data from problem 28 Wolfgang Kersten...

You are given the following five-number summary for a sample 2, 13, 22, 31, 50 What is the LEAST appropriate statement that can be made? a) The standard deviation of the sample is 18.26 b) The...

Marine Products Ltd has identified three possible investment projects. Two of these would have to be started very shortly (Year 0), the third in a years time (Year 1). None of these projects can be...

How innovation is related to technology? Why people interpret innovation differently?

Read the topic Resource "Document Retrieval and Text Retrieval" to enhance your understanding of the process for document and text retrieval. Based on the article, explain how a document and text can...

1. Describe the main purpose of demand forecasting. 2. Explain the different types of forecasting. 3. List out the steps involved in forecasting? 4. Discuss the time series analysis?

1. Review existing strategies implemented at Volvo for Green Building and Energy Technology. (1 point and explanation) 2. Share findings on adequacy, sufficiency, and appropriateness (1 point and...

You have been hired as a Restaurant Manager for a new restaurant in downtown Toronto. The owner, Mr. McDavid, has come to you with a request to incorporate sustainability within the business, both...

1. Discuss the seven factors that should be addressed when making the business case for a new Information System. There are seven factors that should be addressed when making the business case for a...

Una razn de rotacin de activos totales de 3.5 indica que: Por cada $1 en ventas, la empresa adquiri $3.50 en activos durante el Por cada $1 en activos, la empresa gan $3.50 en ingresos netos. Por...

Synthesize the products by drawing out reagents and intermediates along the way. `N H. OH HO HO

A companys machines break down according to a Poisson process at a mean rate of 3 per hour. Nonproductive time on any machine costs the company $60 per hour. The company employs a maintenance person...

Speedy Wheels is a wholesale distributor of bicycles. Its Inventory Manager, Ricky Sapolo, is currently reviewing the inventory policy for one popular model that is selling at the rate of 500 per...

Do Prob. 10.8-2. Reconsider the Tinker Construction Co. problem presented in Prob. 10.8-1. While in college, Sean Murphy took an OR course that devoted a month to linear programming, so Sean has...

Coy and Matt are equal partners in the Matcoy Partnership. Each partner has a basis in his partnership interest of $28,000 at the end of the current year, prior to any distribution. On December 31,...

Pam has a $27,000 basis (including her share of debt) in her 50% partnership interest in the Meddoc partnership before receiving any distributions. This year Meddoc makes a current distribution to...

Two years ago, Kimberly became a 30% partner in the KST Partnership with a contribution of investment land with a $10,000 basis and $16,000 fair market value. On January 2 of this year, Kimberly has...