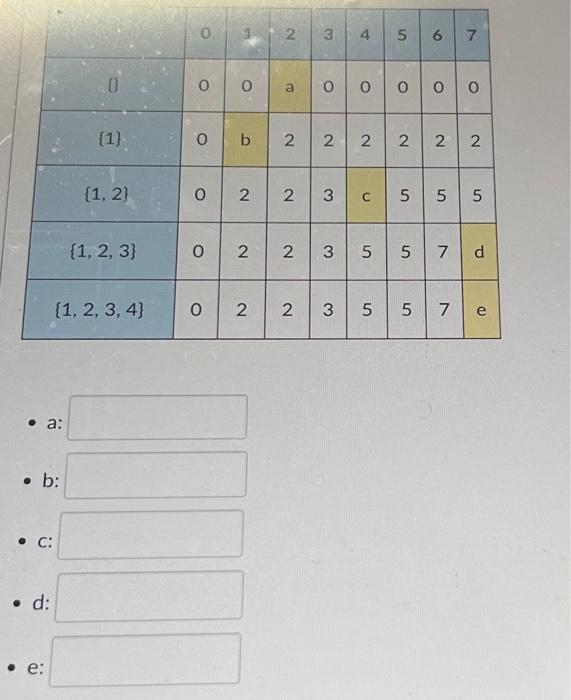
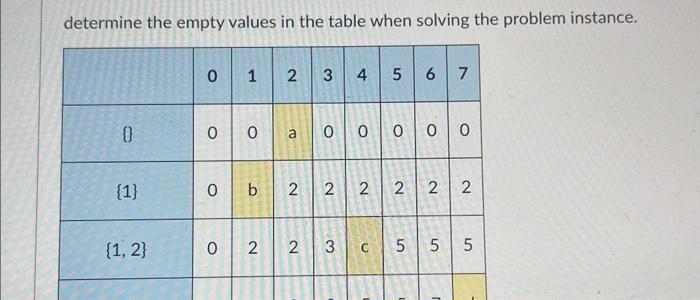
You are solving the 01 Knapsack problem using a Dynamic Programming approach, with the following recurrence relations: OPT(i,W)=0OPT(i,W)=OPT(i1,W)OPT(i,W)=max(OPT(i1,W),vi+OPT(i1,Wwi))ifi=0ifwi>Wotherwise Here, OPT (i,W) represents the optimal value of the knapsack with weight W and i items. vi represents the value of item i and wi represents the weight of item i. The objective is to maximize profit. Given a Knapsack that can hold seven units (W=7) and a choice of four items to relect from - Item 1: value =2, weight =1, - Item 2: value =3, weight =3, - Item 3: value =5, weight =5, - Item 4: value =6, weight =7, determine the empty values in the table when solving the problem instance. \begin{tabular}{|c|c|c|c|c|c|c|c|c|} \hline & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 0 & 0 & 0 & a & 0 & 0 & 0 & 0 & 0 \\ \hline{1} & 0 & b & 2 & 2 & 2 & 2 & 2 & 2 \\ \hline{1,2} & 0 & 2 & 2 & 3 & c & 5 & 5 & 5 \\ \hline{1,2,3} & 0 & 2 & 2 & 3 & 5 & 5 & 7 & d \\ \hline{1,2,3,4} & 0 & 2 & 2 & 3 & 5 & 5 & 7 & e \\ \hline \end{tabular} - a: - b: - C : - d : - e: determine the empty values in the table when solving the problem instance