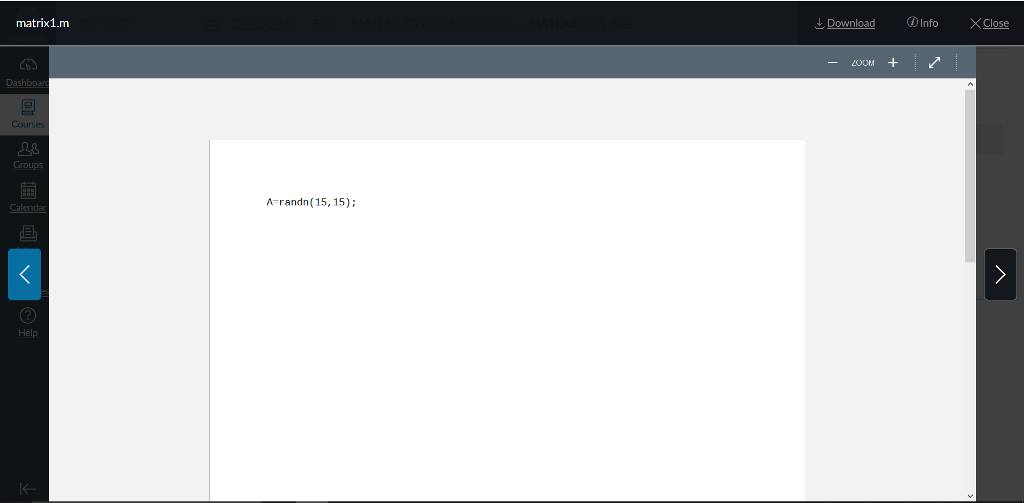
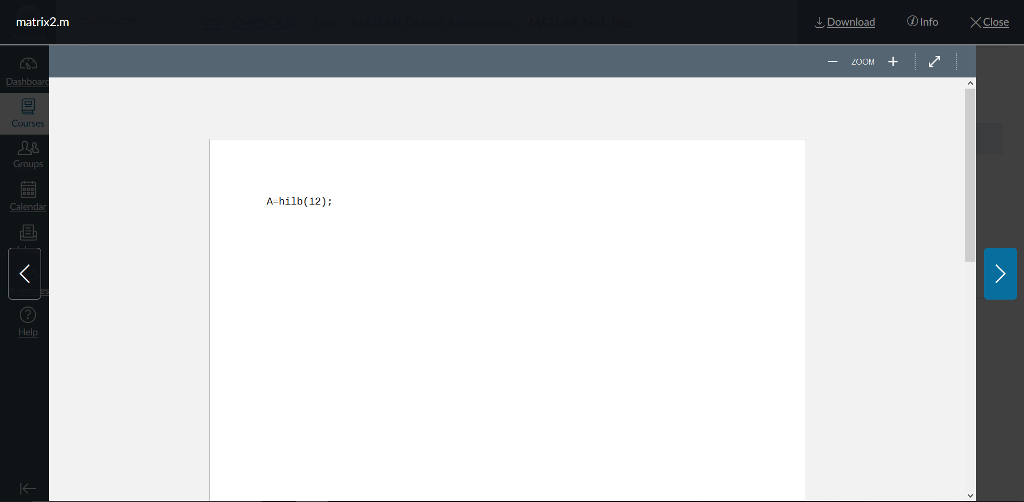
You are to write a MATLAB function to implement the Hager Higham method to estimate the condition number of the matrix A. This is explained in the notes on Canvas and in class. Your function should have the formm [kappa, z,Jcond1(L. U,p,A) Thus, here L, U, and p are outputs from the command [L,U,p]-lu(A, 'vector'). Thus for a given matrix A, you should produce its condition number by the two MATLAB commands [L, U,Pl = lu(A" vector' ); (kappa, z,J cond1(L, U,p, A) Here kappa is the condition number K1 (A) = IAllIA lla, z is the vector such that llzI10-1, IA IA illi = IA TIlo, and J s a column of the identity matrix such that ||AeYou can compute All using MATLAB's norm function and, if you wish, check your result using MATLAB's cond function Your initial guess for z should be Higham's guess which can be generated by the MATLAB code zones(n, 1); signz ; for k 1: n z(k) = signz * (n + k-1); end z = zorm(z, Inf): You are to write a MATLAB function to implement the Hager Higham method to estimate the condition number of the matrix A. This is explained in the notes on Canvas and in class. Your function should have the formm [kappa, z,Jcond1(L. U,p,A) Thus, here L, U, and p are outputs from the command [L,U,p]-lu(A, 'vector'). Thus for a given matrix A, you should produce its condition number by the two MATLAB commands [L, U,Pl = lu(A" vector' ); (kappa, z,J cond1(L, U,p, A) Here kappa is the condition number K1 (A) = IAllIA lla, z is the vector such that llzI10-1, IA IA illi = IA TIlo, and J s a column of the identity matrix such that ||AeYou can compute All using MATLAB's norm function and, if you wish, check your result using MATLAB's cond function Your initial guess for z should be Higham's guess which can be generated by the MATLAB code zones(n, 1); signz ; for k 1: n z(k) = signz * (n + k-1); end z = zorm(z, Inf)