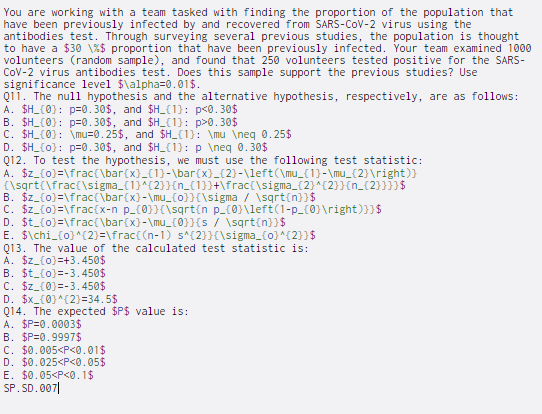
You are working with a team tasked with finding the proportion of the population that have been previously infected by and recovered from SARS-CoV-2 virus using the antibodies test. Through surveying several previous studies, the population is thought to have a $30 \%$ proportion that have been previously infected. Your team examined 1000 volunteers (random sample), and found that 250 volunteers tested positive for the SARS- CoV-2 virus antibodies test. Does this sample support the previous studies? Use significance level $\alpha=0.01$. Q11. The null hypothesis and the alternative hypothesis, respectively, are as follows: A. $H_{0}: p=0.30$, and $H_{1}: p0.30$ C. $H_{0}: \mu=0.25$, and $H_{1}: \mu (neq 0.25$ D. $H_(O): p=0.30$, and $H_{1}: p eq 0.30$ 012. To test the hypothesis, we must use the following test statistic: A. $z_{0}=\frac{\bar{x}_{1}-\bar{x}_{2}-\left\mu_{1}-\mu_{2} ight)} {\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{ \sigma_{2}^{2}}{n_{2}}}}$ B. $z_{0}=\frac{\bar{x}-\mu_{0} }{\sigma / \sqrt{n}}$ C. $z_{0}=\frac{x-n p_{0}}{\sqrt{n p_{0}\left(1-p_{0} ight)}}$ D. $t_{0}=\frac{\bar[x]-\mu_{0}}{5 / \sqrt{n}}$ E. $\chi_{0}^{2}=\frac{(n-1) s^{2}}{\sigma_{0}^{2}}$ Q13. The value of the calculated test statistic is: A. $z_{0} =+3.450$ B. $t_{o}=-3.450$ C. $z_{0}=-3.450$ D. $x_{0}^{2}=34.5$ 014. The expected $P$ value is: A. $P=0.0003$ B. $P=0.9997$ C. $0.005