You can convert any DFA M = ({q0, . . . , qn}, ?, ?, q0, F) into an equivalent CFG as follows. Make a variable Ri for each state qi of the DFA. Add the rule Ri ? aRj to the CFG if ?((qi , a)) = qj is a transition in the DFA. Add the rule Ri ? ? if qi is an accept state of the DFA. Make R0 the start variable of the grammar.

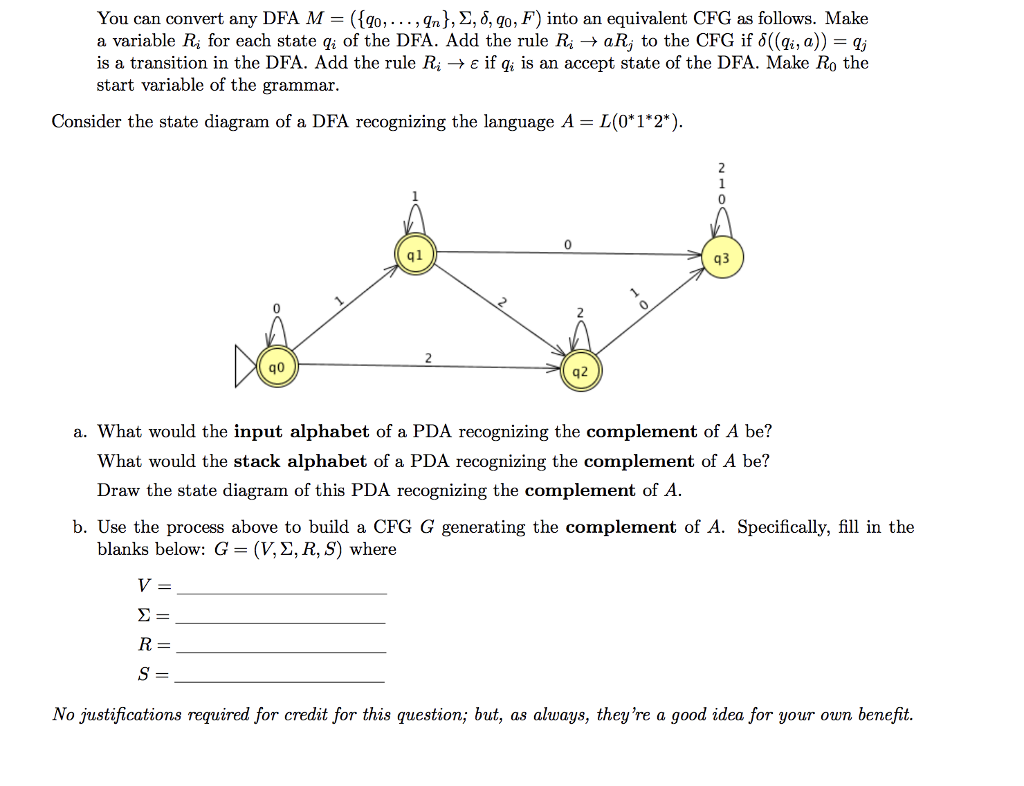
You can convert any DFA M (190, . . . , qn), ?, ?, q0, F) into an equivalent CFG as follows. Make a variable Ri for each state q? of the DFA. Add the rule Ri aRi to the CFG if ?((q a)) If is a transition in the DFA. Add the rule Ri ? if qi is an accept state of the DFA. Make Ro the start variable of the grammar Consider the state diagram of a DFA recognizing the language A - L(0*1*2*) 0 q3 0 q0 q2 a. What would the input alphabet of a PDA recognizing the complement of A be'? What would the stack alphabet of a PDA recognizing the complement of A be? Draw the state diagram of this PDA recognizing the complement of A. b. Use the process above to build a CFG G generating the complement of A. Specifically, fill in the blanks below: G (V, ?, R, S) where No justifications required for credit for this question: but, as alvavs, they're a good idea for your own benefit