you can use random numbers for all DCs if you prefer to do the homework on your own.

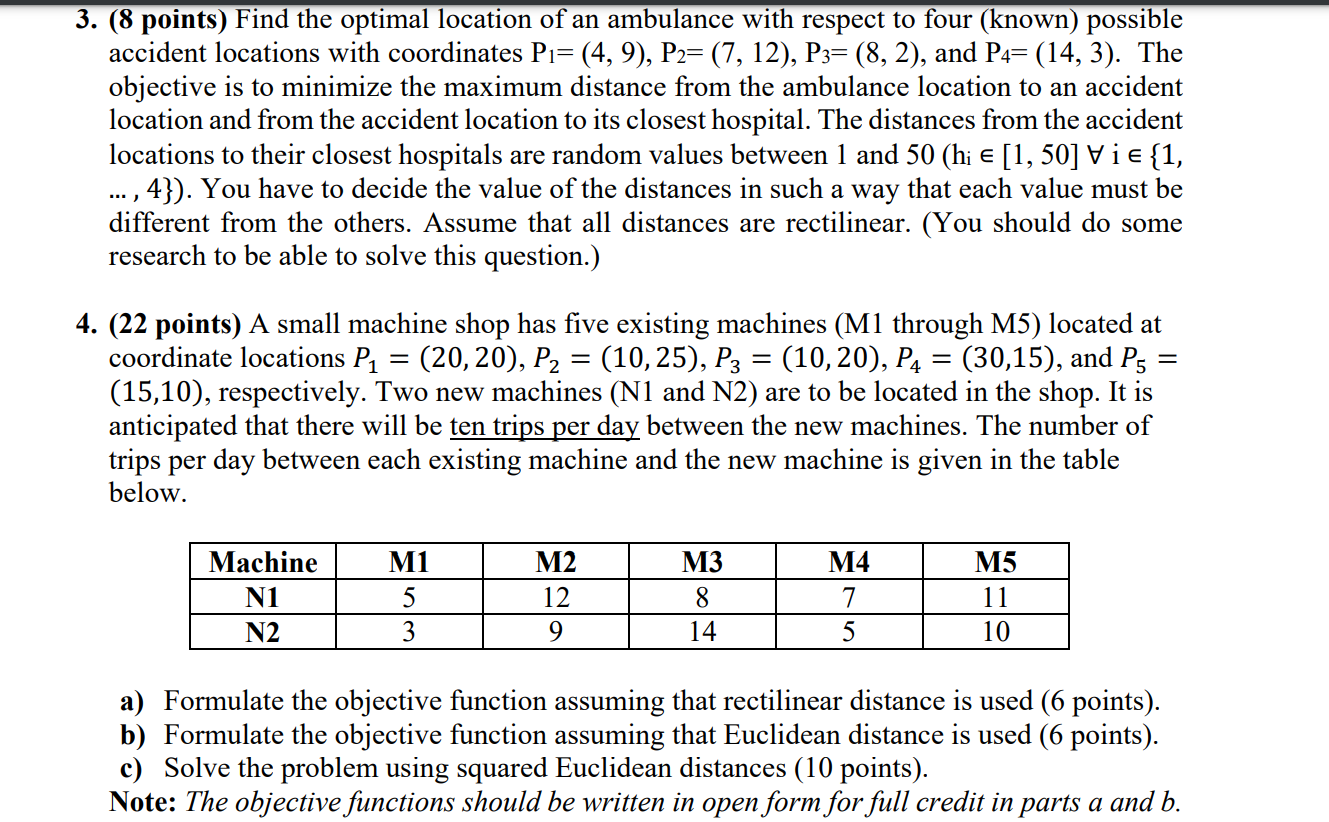
3. (8 points) Find the optimal location of an ambulance with respect to four (known) possible accident locations with coordinates P1=(4,9),P2=(7,12),P3=(8,2), and P4=(14,3). The objective is to minimize the maximum distance from the ambulance location to an accident location and from the accident location to its closest hospital. The distances from the accident locations to their closest hospitals are random values between 1 and 50(hi[1,50]i{1, ,4}). You have to decide the value of the distances in such a way that each value must be different from the others. Assume that all distances are rectilinear. (You should do some research to be able to solve this question.) 4. (22 points) A small machine shop has five existing machines (M1 through M5) located at coordinate locations P1=(20,20),P2=(10,25),P3=(10,20),P4=(30,15), and P5= (15,10), respectively. Two new machines (N1 and N2) are to be located in the shop. It is anticipated that there will be ten trips per day between the new machines. The number of trips per day between each existing machine and the new machine is given in the table below. a) Formulate the objective function assuming that rectilinear distance is used (6 points). b) Formulate the objective function assuming that Euclidean distance is used (6 points). c) Solve the problem using squared Euclidean distances ( 10 points). Note: The objective functions should be written in open form for full credit in parts a and b