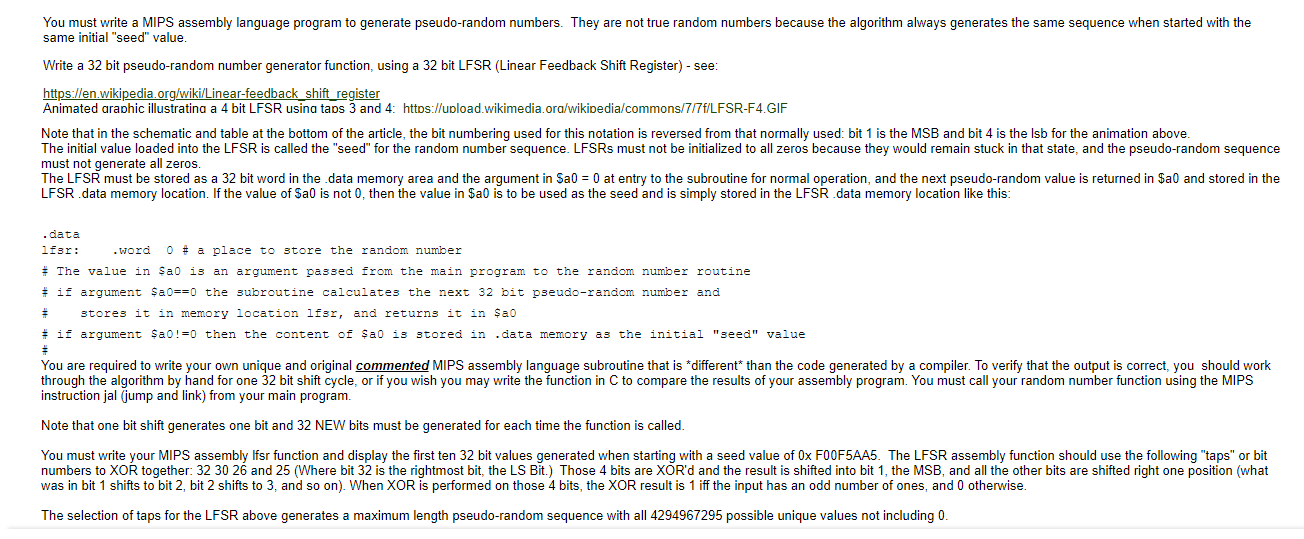
You must write a MIPS assembly language program to generate pseudo-random numbers. They are not true random numbers because the algorithm always generates the same sequence when started with the same initial "seed" value. Write a 32 bit pseudo-random number generator function, using a 32 bit LFSR (Linear Feedback Shift Register) - see: https://en.wikipedia.org/wiki/Linear-feedback_shift_register Animated araphic illustratina a 4 bit LFSR usina taps 3 and 4: https://upload.wikimedia.ora/wikipedia/commons/7/7f/LFSR-F4.GIF Note that in the schematic and table at the bottom of the article, the bit numbering used for this notation is reversed from that normally used: bit 1 is the MSB and bit 4 is the Isb for the animation above. The initial value loaded into the LFSR is called the "seed" for the random number sequence. LFSRs must not be initialized to all zeros because they would remain stuck in that state, and the pseudo-random sequence must not generate all zeros. The LFSR must be stored as a 32 bit word in the data memory area and the argument in Sa0 = 0 at entry to the subroutine for normal operation, and the next pseudo-random value is returned in $a0 and stored in the LFSR data memory location. If the value of Sao is not 0, then the value in $a0 is to be used as the seed and is simply stored in the LFSR data memory location like this: .data 1 for: .word 0 # a place to store the random number # The value in Sao is an argument passed from the main program to the random number routine # if argument $a0==0 the subroutine calculates the next 32 bit pseudo-random number and # stores it in memory location lfsr, and returns it in $ao # if argument $a0!=0 then the content of sao is stored in data memory as the initial "seed" value + You are required to write your own unique and original commented MIPS assembly language subroutine that is different than the code generated by a compiler. To verify that the output is correct, you should work through the algorithm by hand for one 32 bit shift cycle, or if you wish you may write the function in C to compare the results of your assembly program. You must call your random number function using the MIPS instruction jal (jump and link) from your main program Note that one bit shift generates one bit and 32 NEW bits must be generated for each time the function is called. You must write your MIPS assembly Ifsr function and display the first ten 32 bit values generated when starting with a seed value of 0x FO0F5AA5. The LFSR assembly function should use the following "taps" or bit numbers to XOR together: 32 30 26 and 25 (Where bit 32 is the rightmost bit, the LS Bit.) Those 4 bits are XOR'd and the result is shifted into bit 1, the MSB, and all the other bits are shifted right one position (what was in bit 1 shifts to bit 2, bit 2 shifts to 3, and so on). When XOR is performed on those 4 bits, the XOR result is 1 iff the input has an odd number of ones, and otherwise. The selection of taps for the LFSR above generates a maximum length pseudo-random sequence with all 4294967295 possible unique values not including 0. You must write a MIPS assembly language program to generate pseudo-random numbers. They are not true random numbers because the algorithm always generates the same sequence when started with the same initial "seed" value. Write a 32 bit pseudo-random number generator function, using a 32 bit LFSR (Linear Feedback Shift Register) - see: https://en.wikipedia.org/wiki/Linear-feedback_shift_register Animated araphic illustratina a 4 bit LFSR usina taps 3 and 4: https://upload.wikimedia.ora/wikipedia/commons/7/7f/LFSR-F4.GIF Note that in the schematic and table at the bottom of the article, the bit numbering used for this notation is reversed from that normally used: bit 1 is the MSB and bit 4 is the Isb for the animation above. The initial value loaded into the LFSR is called the "seed" for the random number sequence. LFSRs must not be initialized to all zeros because they would remain stuck in that state, and the pseudo-random sequence must not generate all zeros. The LFSR must be stored as a 32 bit word in the data memory area and the argument in Sa0 = 0 at entry to the subroutine for normal operation, and the next pseudo-random value is returned in $a0 and stored in the LFSR data memory location. If the value of Sao is not 0, then the value in $a0 is to be used as the seed and is simply stored in the LFSR data memory location like this: .data 1 for: .word 0 # a place to store the random number # The value in Sao is an argument passed from the main program to the random number routine # if argument $a0==0 the subroutine calculates the next 32 bit pseudo-random number and # stores it in memory location lfsr, and returns it in $ao # if argument $a0!=0 then the content of sao is stored in data memory as the initial "seed" value + You are required to write your own unique and original commented MIPS assembly language subroutine that is different than the code generated by a compiler. To verify that the output is correct, you should work through the algorithm by hand for one 32 bit shift cycle, or if you wish you may write the function in C to compare the results of your assembly program. You must call your random number function using the MIPS instruction jal (jump and link) from your main program Note that one bit shift generates one bit and 32 NEW bits must be generated for each time the function is called. You must write your MIPS assembly Ifsr function and display the first ten 32 bit values generated when starting with a seed value of 0x FO0F5AA5. The LFSR assembly function should use the following "taps" or bit numbers to XOR together: 32 30 26 and 25 (Where bit 32 is the rightmost bit, the LS Bit.) Those 4 bits are XOR'd and the result is shifted into bit 1, the MSB, and all the other bits are shifted right one position (what was in bit 1 shifts to bit 2, bit 2 shifts to 3, and so on). When XOR is performed on those 4 bits, the XOR result is 1 iff the input has an odd number of ones, and otherwise. The selection of taps for the LFSR above generates a maximum length pseudo-random sequence with all 4294967295 possible unique values not including 0