you solution this question before but Regarding 5.1 assuming the matrix already input (there is no need to input matrix) Just a simple solution how to write O(n^2) program.... and didn't answer all the questions

what the information you need it?

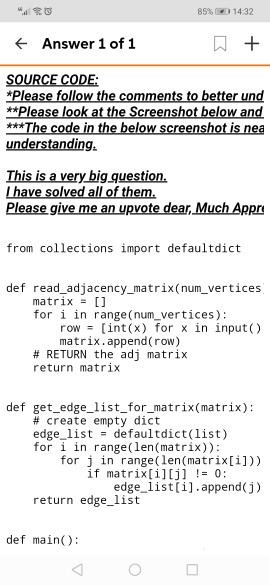
4 Recognizing a star (20 points) A graph G is a star if it has a vertex r adjacent to every other vertex and ris the only neighbour of every other vertex. Given the adjacency matrix of a graph G, design an O(na) algorithms that prints YES if G is a star and NO otherwise. 5 Processing the list of edges 5.1 Listing all the edges (5 points) Write an O(n) program whose input is the adjacency matrix of a graph G. The program should print the list of all the edges (without repetition). For example, if the vertices of the graph are 0, 1,2,3,4,5 with O adjacent to 1 and 5, 1 adjacent to 5 2 adjacent to 3 and 4 and 3 adjacent to 4 then the printed list should be something like. 5.2 Removal of an edge (5 points) Let G be a graph and e be an edge of G. We denote by Ge the graph obtained from G by removal fo e. That is, the vertices of G\e are the same as in G and the edges of G\e are all the edges of G but e. Write a program whose input is the adjacency matrix of a graph G and two vertices i and such that that are adjacent in G. The program should print the adjacency matrix of G\{ij} (that is G with the edge between i and j being removed). 5.3 Listing all the bridges (10 points) Let G be a connected graph and e be an edge of G. We say that e is a bridge of Gif G e is not connected put it differently, the removal of e breaks the connectivity of G). Assume that we have a function Connect whose input is the adjacency matrix of a graph and the output is true if the graph is connected and false otherwise. Using this procedure, design an algorithm that prints all the bridges of G. Hint: Use the algorithm for the first part of that question for exploration of all the edges. Rather than printing the curretly considered edge straightaway, use the Connect procedure to check whether the given edges is a bridge (the 85% 14:32 + Answer 1 of 1 + SOURCE CODE: *Please follow the comments to better und **Please look at the Screenshot below and ***The code in the below screenshot is nea understanding. This is a very big question. I have solved all of them. Please give me an upvote dear, Much Appre from collections import defaultdict def read_adjacency_matrix(num_vertices matrix = [] for i in range(num_vertices): row = (int(x) for x in input() matrix.append(row) # RETURN the adj matrix return matrix def get_edge_list_for_matrix(matrix): # create empty dict edge_list = defaultdict(list) for i in range(len(matrix)): for j in range (len(matrix[i])) if matrix[i][j] != 0: edge_list[i].append(j) return edge_list def main()