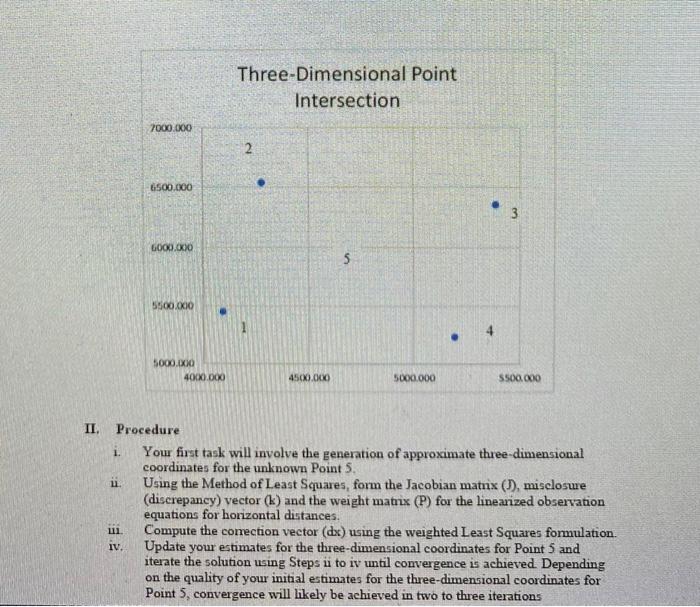
You will be computing the best estimate for the three-dimensional coordinates for Point 5 using four distances measured from Points 1. 2. 3 and 4 as per the tables and diagram given below. Point 1 2 3 X (m) 4093.320 4280.277 5384.999 5192.832 4730.000 Y(m) 5453.387 6542.468 6357.830 5239.205 5900.000 z (m) 245.705 243.158 246.991 244.660 440.000 4 4 5 from / to 1 to 5 2 to 5 3 to 5 4 to 5 Distance 802.717 810.199 822.980 830.415 std, dev. 0.004 0.004 0.004 0.004 Three-Dimensional Point Intersection 7000.000 2 6500.000 3 6000.000 5 55000 5000.X 4000.000 450.000 5000.000 S500.000 1. II. Procedure Your first task will involve the generation of approximate three-dimensional coordinates for the unknown Point S. u. Using the Method of Least Squares, form the Jacobian matrix (), misclosure (discrepancy) vector (k) and the weight matrix (P) for the linearized observation equations for horizontal distances. Compute the correction vector (dx) using the weighted Least Squares formulation. Update your estimates for the three-dimensional coordinates for Point 5 and iterate the solution using Steps i to iv until convergence is achieved. Depending on the quality of your initial estimates for the three-dimensional coordinates for Point 5, convergence will likely be achieved in two to three iterations 11 IV. You will be computing the best estimate for the three-dimensional coordinates for Point 5 using four distances measured from Points 1. 2. 3 and 4 as per the tables and diagram given below. Point 1 2 3 X (m) 4093.320 4280.277 5384.999 5192.832 4730.000 Y(m) 5453.387 6542.468 6357.830 5239.205 5900.000 z (m) 245.705 243.158 246.991 244.660 440.000 4 4 5 from / to 1 to 5 2 to 5 3 to 5 4 to 5 Distance 802.717 810.199 822.980 830.415 std, dev. 0.004 0.004 0.004 0.004 Three-Dimensional Point Intersection 7000.000 2 6500.000 3 6000.000 5 55000 5000.X 4000.000 450.000 5000.000 S500.000 1. II. Procedure Your first task will involve the generation of approximate three-dimensional coordinates for the unknown Point S. u. Using the Method of Least Squares, form the Jacobian matrix (), misclosure (discrepancy) vector (k) and the weight matrix (P) for the linearized observation equations for horizontal distances. Compute the correction vector (dx) using the weighted Least Squares formulation. Update your estimates for the three-dimensional coordinates for Point 5 and iterate the solution using Steps i to iv until convergence is achieved. Depending on the quality of your initial estimates for the three-dimensional coordinates for Point 5, convergence will likely be achieved in two to three iterations 11 IV