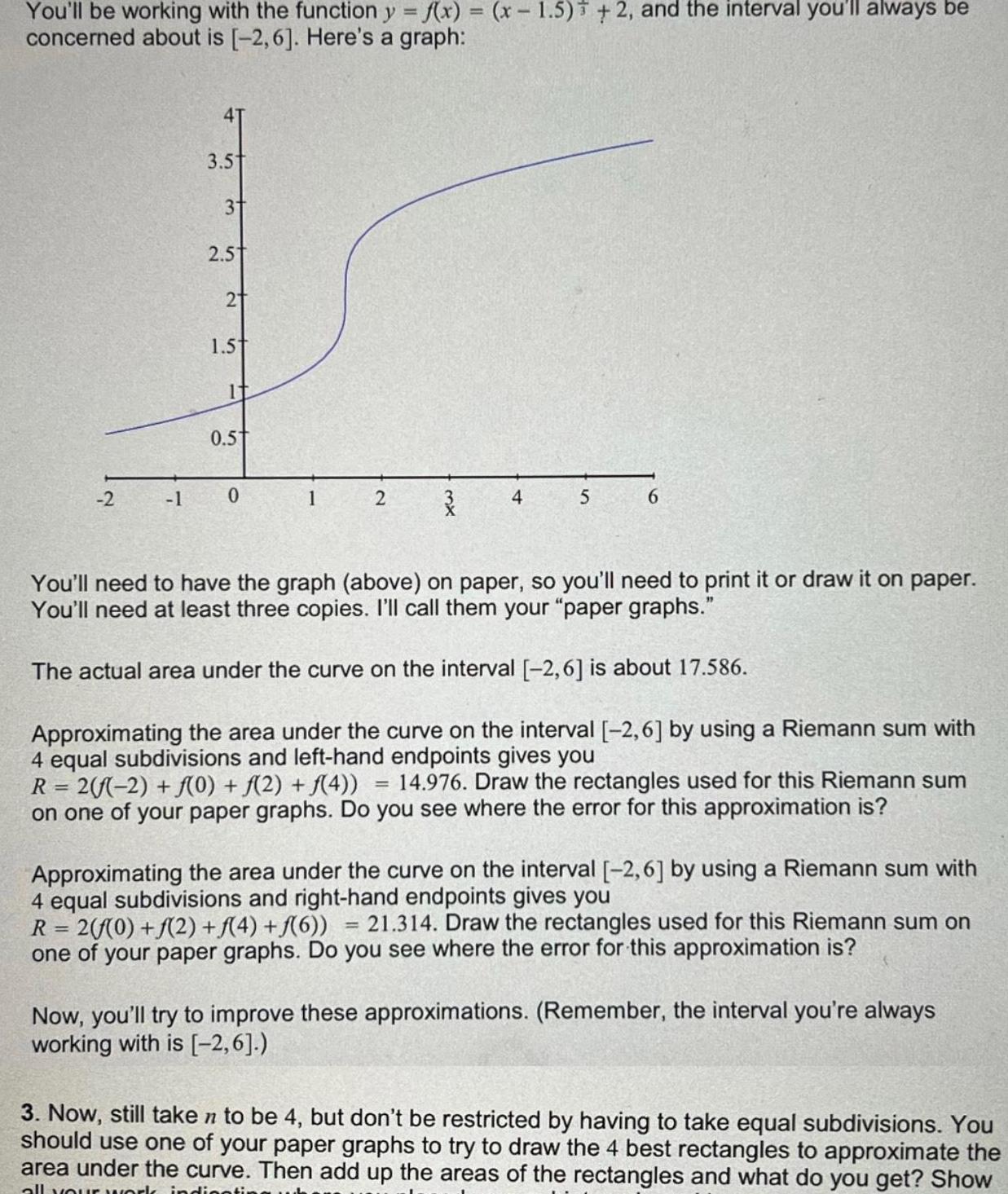
You'll be working with the function y = f(x) = (x - 1.5) +2, and the interval you'll always be concerned about is [-2,6]. Here's a graph: 3.5 31 2.5 21 1.5 0.5 -2 -1 0 1 2 4 5 6 You'll need to have the graph (above) on paper, so you'll need to print it or draw it on paper. You'll need at least three copies. I'll call them your "paper graphs." The actual area under the curve on the interval [-2,6] is about 17.586. Approximating the area under the curve on the interval [-2,6] by using a Riemann sum with 4 equal subdivisions and left-hand endpoints gives you R=2((-2)+f(0) + f(2) + f(4)) = 14.976. Draw the rectangles used for this Riemann sum on one of your paper graphs. Do you see where the error for this approximation is? Approximating the area under the curve on the interval [-2,6] by using a Riemann sum with 4 equal subdivisions and right-hand endpoints gives you = R=2(f(0)+(2) +(4) +(6)) 21.314. Draw the rectangles used for this Riemann sum on one of your paper graphs. Do you see where the error for this approximation is? Now, you'll try to improve these approximations. (Remember, the interval you're always working with is [-2,6].) 3. Now, still take n to be 4, but don't be restricted by having to take equal subdivisions. You should use one of your paper graphs to try to draw the 4 best rectangles to approximate the area under the curve. Then add up the areas of the rectangles and what do you get? Show all your work indicatin