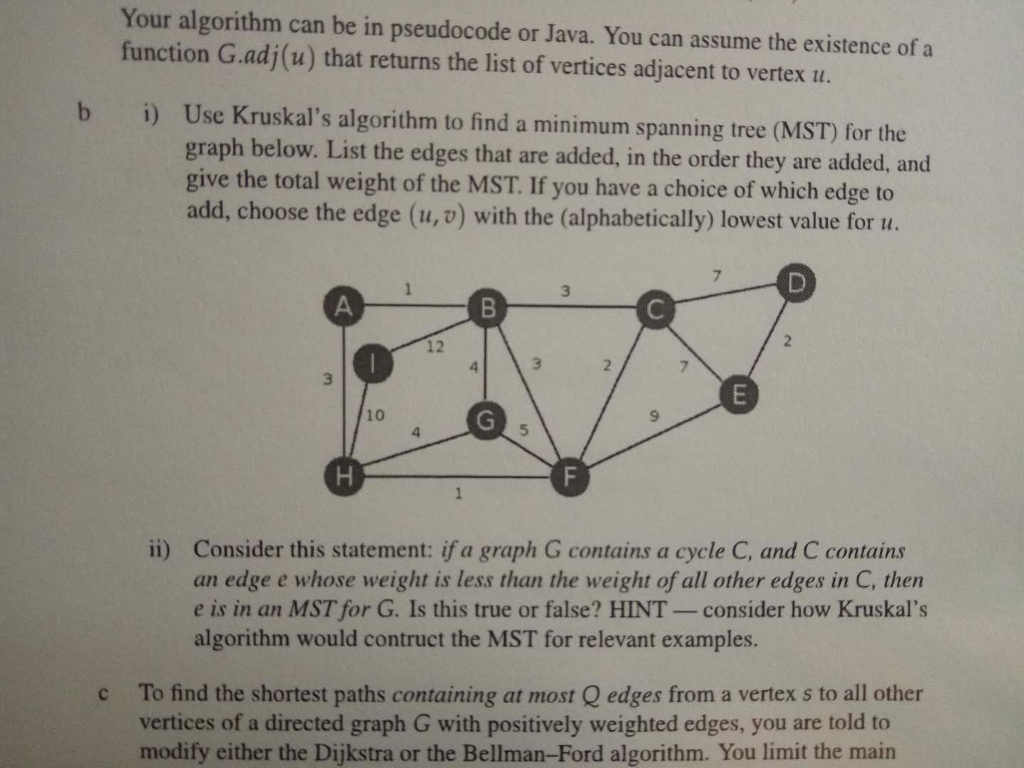
Your algorithm can be in pseudocode or Java. You can assume the existence of a function G.adj(u) that returns the list of vertices adjacent to vertex u. b i) Use Kruskal's algorithm to find a minimum spanning tree (MST) for the graph below. List the edges that are added, in the order they are added, and give the total weight of the MST. If you have a choice of which edge to add, choose the edge (u, v) with the (alphabetically) lowest value for u. 3 12 10 9 Consider this statement: if a graph G contains a cycle C, and C contains an edge e whose weight is less than the weight of all other edges in C, then e is in an MST for G. Is this true or false? HINT-consider how Kruskal's algorithm would contruct the MST for relevant examples. ii) To find the shortest paths containing at most Q edges from a vertex s to all other vertices of a directed graph G with positively weighted edges, you are told to modify either the Dijkstra or the Bellman-Ford algorithm. You limit the main c