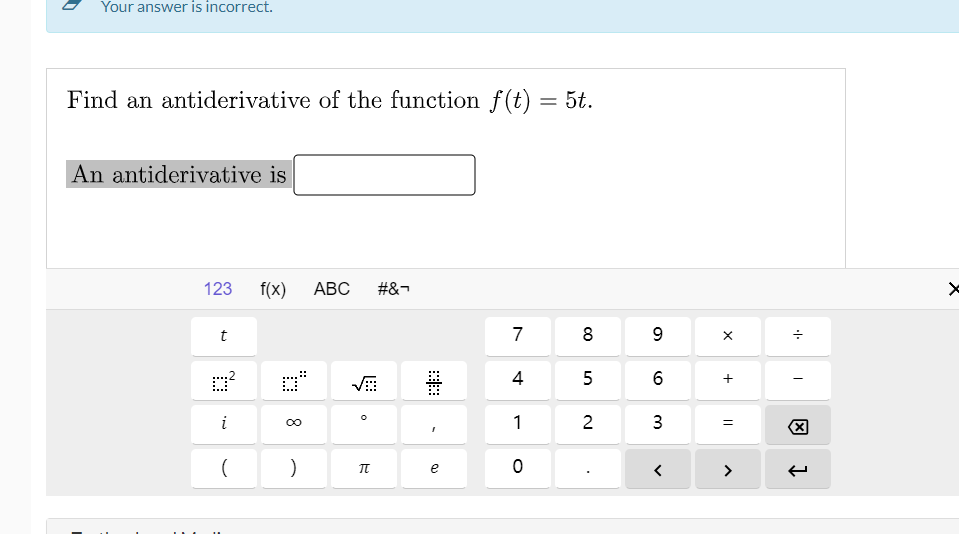
Question: Your answer is incorrect. Find an antiderivative of the function f (t) = 5t. An antiderivative is 123 f(x) ABC #&7 X r+ 7 8
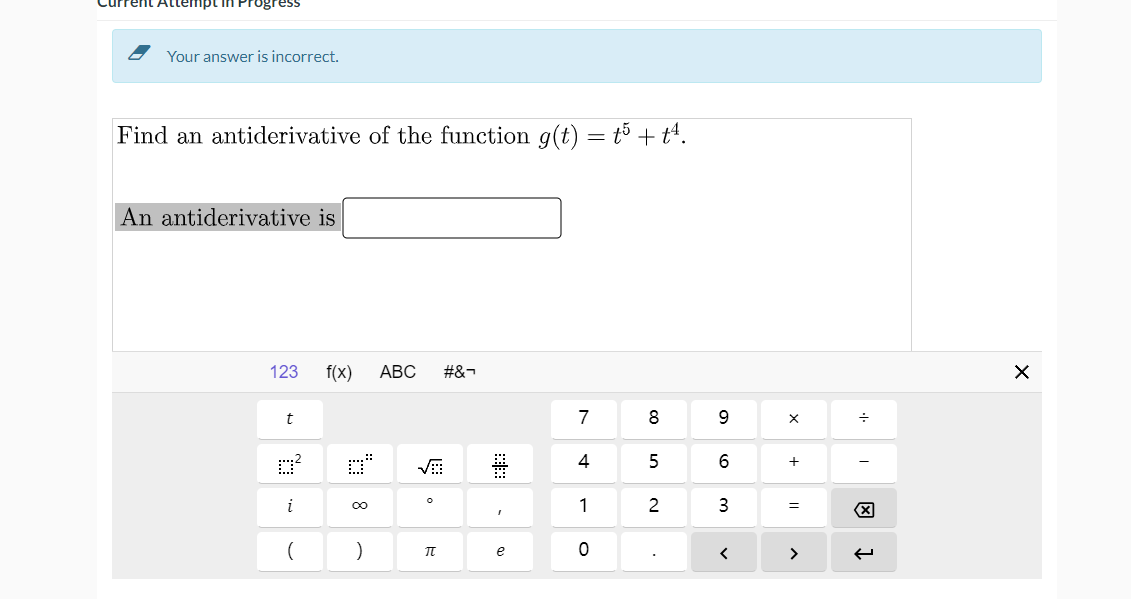




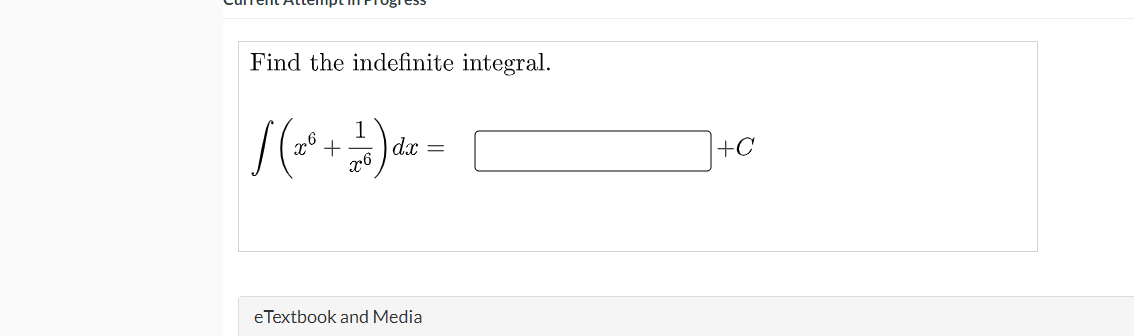

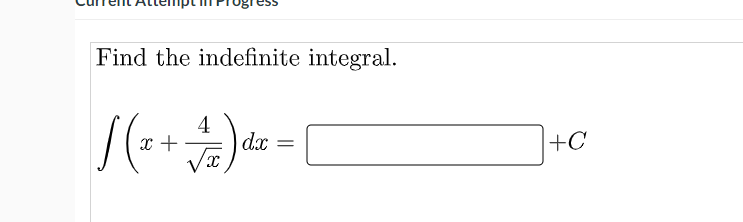

Your answer is incorrect. Find an antiderivative of the function f (t) = 5t. An antiderivative is 123 f(x) ABC #&7 X r+ 7 8 9 X : 2 4 5 6 + 2 = (X e 0 Current Attempt in Your answer is incorrect. Find an antiderivative of the function g(t) = to + 14. An antiderivative is 123 f(x) ABC #&7 X t 7 8 9 X 4 5 6 + N = X e 0 >Find an antiderivative of the following function. f (a) = 5 An antiderivative isFind an antiderivative of the function g(x) = 1023 + 10. An antiderivative is eTextbook and Media\fFind the indefinite integral. +C\fOver the past fty years the carbon dioxide level in the atmosphere has increased. Carbon dioxide is believed to drive temperature, so predictions of future carbon dioxide levels are important. If C(t) is carbon dioxide level in parts per million (ppm) and t is time in years since 1950, three possible models arel: I. 01:) = 1.3 II. C'(t) = 0.5 + 0.03: III. cm) = 0.5eD-DDD (a) Given that the carbon dioxide level was 314 ppm in 1950, nd C(t) for each model. we: W: we: (b) Find the carbon dioxide level in 2020 predicted by each model. Round your answer to two decimal places if necessary. Model I predicts 0=|:|DDDD Model II predicts C l:|pp1 |:|DDDD Model III predicts C
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


