Your client, a man, is currently 35 year old and he wants to retire when he is 65 years

old (exactly 30 years from now). He would like his retirement income to be equivalent to

$6,000 per month, adjusted for inflation. You estimate the inflation rate for the next 30

years to average 3% annually. He anticipates purchasing a guaranteed retirement annuity

from an insurance company the month before he retires (359 months from now). The

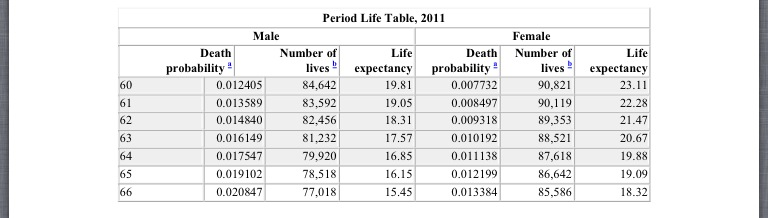
insurance company will use the actuarial life expectancy table below to determine the

cost of the annuity. As you can see, he is expected to live about 16 years (so, he should

expect to purchase a 193 month annuity) following retirement. They will add a 4%

premium to the pure premium calculated from their actuarial table.He has $25,000 in

savings today that will be invested until he retires. Given a rate of return of 6% (annually

but compounded monthly) for the foreseeable future for both your client and the

insurance company, how much does he need to save each month (359 months) for the

next 29 years and 11 months (first payment to be made in one month) if he is to afford to

purchase the annuity contract? (Assume that you make the last monthly payment in 29

years and 11 months, the month before you receive your first monthly retirement

payment)

1) What dollar amount will be needed per month at retirement age? (HINT: You

want the equivalent to 6,000 per month when you retire; however, inflation will

be 3% over the next 30 years! So you want to calculate the FV in 30 years.)

FV30 years =

2) OK, in part (1) you calculated the monthly dollar amount needed for retirement.

Now you need to determine what the PV of this stream of retirement income will

be (one month before retirement). HINT: This will be the PVA of the stream of

monthly retirement income from part (1) for 193 months. Remember this PV

is in the future when you are ready to retire.)

PVAmonth359 = PVA193 months=

3) What will the price of this annuity? (HINT: This next step is easy you need to

determine what this annuity will cost. The figure you arrived at in part (2) is the

pure premium. Now you need to increase this by the amount the insurance

company adds to the pure premium.)

Price =PVAmonth359x Premium =

4) What is the future value of your clients savings in 359 months when he plans to

retire? (HINT: Your client has savings what will these be worth in the future?)

FV359 months =

5) What is the new total amount needed by month 359 when he plans to retire? (HINT:

This is easy to calculate it is the amount from (3) minus the figure determined in

(4).)

6) How much needs to be saved monthly so you will have sufficient savings to

purchase this annuity from the insurance company? (HINT: You need to solve for

the annuity amount. You know the FVA, the interest rate, number of periods.)