Your Tasks:

1. Create a class Polynomial that has the following characteristics.
   • Attributes
     • degree: int - the degree of the Polynomial. Polynomial is zero, consider degree -1. If the degree given by the user is negative, multiply by -1 (you could throw and exception but we will not do it in this exercise)
     • coefficients: int[] - array holding the coefficients of the polynomial
   • Methods
     • constructor with arguments for both attributes
     • adjustPoly(): void - a method that adjusts the degree of the polynomial if the value of the coefficients of the highest degree is zero. The array of coefficients hold the coefficients corresponding to the power of the x, index 0 holds coefficient for x^0 and index length-1 holds the coefficient for x^degree. The method also adjusts the array coefficients.
     • accessor methods for degree and coefficients
     • evaluate(int x): int - method that evaluates the value of the Polynomial for a given value for x
     • addPoly(Polynomial p): Polynomial - method that adds the current Polynomial object with a Polynomial p, and returns the sum of the two polynomials, as a Polynomial object.
     • subtractPoly(Polynomial p): Polynomial - method that subtracts Polynomial p from the current object of type Polynomial
     • derivative(): Polynomial - method that calculates the derivative of the current object of type Polynomial.
     • equals(Polynomial p): boolean - method that returns true if the current calling object and p are equal, meaning they have same degree, and same coefficients
     • toString(): String - method that returns a String representing the polynomial, written starting with highest power of x. Use x as variable, and ^ for the power. Sample returned String: 2x^4 - x^3 + 4x^2 + x + 5, for Polynomial object having degree=4, and coefficients={5, 1, 4, -1, 2}
2. Create a driver class named PolynomialDriver to test the Polynomial class, in which you perform the following tasks:
   • Define a polynomial zero, with value zero.
   • Define and instantiate a Polynomial object p1 with degree 4, and random coefficients between 0 and 10.
   • Define and instantiate another Polynomial object p2 with degree 3, and random coefficients between 0 and 10.
   • Add polynomials p1 and p2 and display the result.
   • Subtract polynomial p1 from polynomial zero, and display the result.
   • Evaluate p1 for x=2 and display the result.
   • Check if p1 and p2 are equal.
   • Calculate the derivative of polynomial p1 and display the result.
3. Run the program and capture a snapshot of the results.
4. If you implement all the required methods properly, the program should generate outputs similar to the following:

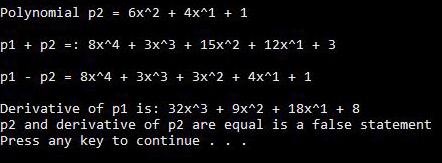
Polynomial p2 = 6x^2 + 4x^1 + 1 p1 + P2 =: 8x^4 + 3x^3 + 15x^2 + 12x^1 + 3 p1 - p2 = 8x^4 + 3x^3 + 3x^2 + 4x^1 + 1 Derivative of p1 is: 32x^3 + 9x^2 + 18x^1 + 8 p2 and derivative of p2 are equal is a false statement Press any key to continue