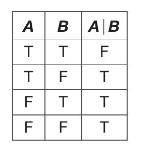
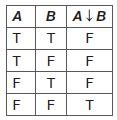
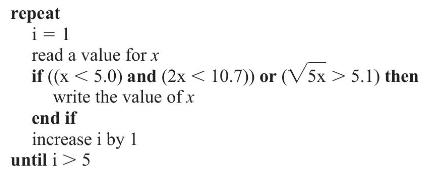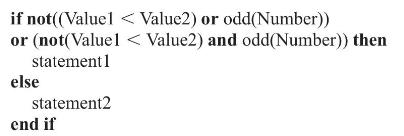Mathematical Structures For Computer Science Discrete Mathematics And Its Applications 7th Edition Judith L. Gersting - Solutions

Unlock the full potential of "Mathematical Structures for Computer Science: Discrete Mathematics and Its Applications, 7th Edition" by Judith L. Gersting with our comprehensive resources. Discover online answers key, detailed answers, and a solution manual tailored for each chapter. Our solutions PDF offers solved problems and questions and answers designed to enhance your understanding. Delve into the test bank and chapter solutions for a thorough grasp, while step-by-step answers guide your learning process. Perfect for students and instructors, our textbook resources, including the instructor manual, are available for free download to support your educational journey.

Which of the following sentences are statements?a. The moon is made of green cheese.b. He is certainly a tall man.c. Two is a prime number.d. The game will be over by 4:00.e. Next year interest rates will rise.f. Next year interest rates will fall.g. \(x^{2}-4=0\)
What is the truth value of each of the following statements?a. 8 is even or 6 is odd.b. 8 is even and 6 is odd.c. 8 is odd or 6 is odd.d. 8 is odd and 6 is odd.e. If 8 is odd, then 6 is odd.f. If 8 is even, then 6 is odd.g. If 8 is odd, then 6 is even.h. If 8 is odd and 6 is even, then \(8
Given the truth values \(A\) true, \(B\) false, and \(C\) true, what is the truth value of each of the following wffs?a. \(A \wedge(B \vee C)\)b. \((A \wedge B) \vee C\)c. \((A \wedge B)^{\prime} \vee C\)d. \(A^{\prime} \vee\left(B^{\prime} \wedge C \right)^{\prime}\)
Given the truth values \(A\) false, \(B\) true, and \(C\) true, what is the truth value of each of the following wffs?a. \(A \rightarrow(B \vee C)\)b. \((A \vee B) \rightarrow C\)c. \(C \rightarrow\left(A^{\prime} \wedge B^{\prime}\right)\)d. \(A \vee\left(B^{\prime} \rightarrow C \right)\)
Rewrite each of the following statements in the form "If \(A\), then \(B\)."a. Healthy plant growth follows from sufficient water.b. Increased availability of information is a necessary condition for further technological advances.c. Errors were introduced only if there was a modification of the
Rewrite each of the following statements in the form "If \(A\), then \(B\)."a. Candidate Lu winning the election will be a sufficient condition for property taxes to increase.b. The user clicks Pause only if the game level changes.c. The components are scarce, therefore the price increases.d.
Common English has many ways to describe logical connectives. Write a wff for each of the following expressions.a. Either \(A\) or \(B\)b. Neither \(A\) nor \(B\)
Common English has many ways to describe logical connectives. Write a wff for each of the following expressions.a. \(B\) whenever \(A\)b. \(A\) is derived from \(B\)c. \(A\) indicates \(B\)d. \(A\) exactly when \(B\)
Several forms of negation are given for each of the following statements. Which are correct?a. The answer is either 2 or 3.1. Neither 2 nor 3 is the answer.2. The answer is not 2 or not 3.3. The answer is not 2 and it is not 3.b. Cucumbers are green and seedy.1. Cucumbers are not green and not
Several forms of negation are given for each of the following statements. Which are correct?a. The carton is sealed or the milk is sour.1. The milk is not sour or the carton is not sealed.2. The carton is not sealed and also the milk is not sour.3. If the carton is not sealed, then the milk will be
Write the negation of each statement.a. If the food is good, then the service is excellent.b. Either the food is good or the service is excellent.c. Either the food is good and the service is excellent, or else the price is high.d. Neither the food is good nor the service excellent.e. If the price
Write the negation of each statement.a. The processor is fast but the printer is slow.b. The processor is fast or else the printer is slow.c. If the processor is fast, then the printer is slow.d. Either the processor is fast and the printer is slow, or else the file is damaged.e. If the file is not
Using the letters indicated for the component statements, translate the following compound statements into symbolic notation.a. A: prices go up; B: housing will be plentiful; C: housing will be expensive If prices go up, then housing will be plentiful and expensive; but if housing is not expensive,
Using the letters indicated for the component statements, translate the following compound statements into symbolic notation.a. A: the tractor wins; B: the truck wins; C: the race will be exciting.Whether the tractor wins or the truck wins, the race will be excitingb. A: snow; B: rain; C: yesterday
Let A, B, and C be the following statements:A Roses are red.B Violets are blue.C Sugar is sweet.Translate the following compound statements into symbolic notation.a. Roses are red and violets are blue.b. Roses are red, and either violets are blue or sugar is sweet.c. Whenever violets are blue,
Let A, B, and C, and D be the following statements:A The villain is French.B The hero is American.C The heroine is British.D The movie is good.Translate the following compound statements into symbolic notation.a. The hero is American and the movie is good.b. Athough the villain is French, the movie
Use \(A, B\), and \(C\) as defined in Exercise 15 to translate the following statements into English.Data from in exercise 15Let A, B, and C be the following statements:A Roses are red.B Violets are blue.C Sugar is sweet.a. \(B \vee C^{\prime}\)b. \(B^{\prime} \vee(A \rightarrow C)\)c. \(\left(C
Use \(A, B\), and \(C\) as defined in Exercise 16 to translate the following statements into English.Data from in Exercise 16Let A, B, and C, and D be the following statements:A The villain is French.B The hero is American.C The heroine is British.D The movie is good.a. \(B \rightarrow
Using letters \(H, K, A\) for the component statements, translate the following compound statements into symbolic notation.a. If the horse is fresh, then the knight will win.b. The knight will win only if the horse is fresh and the armor is strong.c. A fresh horse is a necessary condition for the
Using letters A, T, E for the component statements, translate the following compound statements into symbolic notation.a. If Anita wins the election, then tax rates will be reduced.b. Tax rates will be reduced only if Anita wins the election and the economy remains strong.c. Tax rates will be
Using letters F, B, S for the component statements, translate the following compound statements into symbolic notation.a. Plentiful fish are a sufficient condition for bears to be happy.b. Bears are happy only if there are plentiful fish.c. Unhappy bears means that the fish are not plentiful and
Using letters P, C, B, L for the component statements, translate the following compound statements into symbolic notation.a. If the project is finished soon, then the client will be happy and the bills will be paid.b. If the bills are not paid, then the lights will go out.c. The project will be
Construct truth tables for the following wffs. Note any tautologies or contradictions.a. \((A \rightarrow B) \leftrightarrow A^{\prime} \vee B\)b. \((A \wedge B) \vee C \rightarrow A \wedge(B \vee C)\)c. \(A \wedge\left(A^{\prime} \vee B^{\prime} \right)^{\prime}\)d. \(A \wedge B \rightarrow
Construct truth tables for the following wffs. Note any tautologies or contradictions.a. \(A \rightarrow(B \rightarrow A)\)b. \(A \wedge B \leftrightarrow B^{\prime} \vee A^{\prime}\)c. \(\left(A \vee B^{\prime}\right) \wedge(A \wedge B)^{\prime}\)d. \(\left[(A \vee B) \wedge C^{\prime}\right]
Verify the equivalences in the list on page 9 by constructing truth tables. (We have already verified \(1 \mathrm{a}, 4 \mathrm{~b}\), and \(5 \mathrm{a}\).)
Verify by constructing truth tables that the following wffs are tautologies. Note that the tautologies in parts \(\mathrm{b}, \mathrm{e}, \mathrm{f}\), and \(\mathrm{g}\) produce equivalences such as \(\left(A^{\prime}\right)^{\prime} \Leftrightarrow A\).a. \(A \vee A^{\prime}\)b.
Prove the following tautologies by starting with the left side and finding a series of equivalent wffs that will convert the left side into the right side. You may use any of the equivalencies in the list on page 9 or the equivalencies from Exercise 26.a. \(\left(A \wedge B^{\prime}\right) \wedge C
Prove the following tautologies by starting with the left side and finding a series of equivalent wffs that will convert the left side into the right side. You may use any of the equivalencies in the list on page 9 or the equivalencies from Exercise 26.a. \(\left(A \wedge B^{\prime}\right)^{\prime}
We mentioned that \((A \wedge B) \vee C\) cannot be proved equivalent to \(A \wedge(B \vee C)\) using either of the associative tautological equivalences, but perhaps it can be proved some other way. Are these two wffs equivalent? Prove or disprove.
Let \(P\) be the wff \(A \rightarrow B\). Prove or disprove whether \(P\) is equivalent to any of the following related wffs.a. the converse of \(P, B \rightarrow A\)b. the inverse of \(P, A^{\prime} \rightarrow B^{\prime}\)c. the contrapositive of \(P, B^{\prime} \rightarrow A^{\prime}\)
Write a logical expression for a Web search engine to find sites pertaining to dogs that are not retrievers.
Write a logical expression for a Web search engine to find sites pertaining to oil paintings by Van Gogh or Rembrandt but not Vermeer.
Write a logical expression for a Web search engine to find sites pertaining to novels or plays about AIDS.
Write a logical expression for a Web search engine to find sites pertaining to coastal wetlands in Louisiana but not in Alabama.
Consider the following pseudocode.The input values for x are 1.0, 5.1, 2.4, 7.2, and 5.3. What are the output values? repeat i = 1 read a value for x if ((x < 5.0) and (2x < 10.7)) or (5x>5.1) then write the value of x end if increase i by 1 until i > 5
Suppose that A, B, and C represent conditions that will be true or false when a certain computer program is executed. Suppose further that you want the program to carry out a certain task only when A or B is true (but not both) and C is false. Using A, B, and C and the connectives AND, OR, and NOT,
Rewrite the following statement form with a simplified conditional expression, where the function returns true if is odd. if not((Value1 or (not(Value1 statement 1 else end if statement2 < Value2) or odd(Number)) < Value2) and odd(Number)) then
You want your program to execute statement 1 when AA is false, BB is false, and CC is true, and to execute statement 2 otherwise. You wrote \section*{if not(Anot⁡(A and B)B) and CC then}statement 1elsestatement 2end ifDoes this do what you want?
Verify that \(A \rightarrow B\) is equivalent to \(A^{\prime} \vee B\).
a. Using Exercise 39 and other equivalences, prove that the negation of \(A \rightarrow B\) is equivalent to \(A \wedge B^{\prime}\)b. Write the negation of the statement "If Sam passed his bar exam, then he will get the job."Data from in exercise 39Verify that \(A \rightarrow B\) is equivalent to
Use algorithm TautologyTest to prove that the following expressions are tautologies.a. \(\left[B^{\prime} \wedge(A \rightarrow B)\right] \rightarrow A^{\prime}\)b. \([(A \rightarrow B) \wedge A] \rightarrow B\)c. \((A \vee B) \wedge A^{\prime} \rightarrow B\)
Use algorithm TautologyTest to prove that the following expressions are tautologies.a. \((A \wedge B) \wedge B^{\prime} \rightarrow A\)b. \(\left(A \wedge B^{\prime}\right) \rightarrow(A \rightarrow B)^{\prime}\)c. \((A \wedge B)^{\prime} \vee B^{\prime} \rightarrow A^{\prime} \vee B^{\prime}\)
A memory chip from a digital camera has \(2^{5}\) bistable (ON-OFF) memory elements. What is the total number of ON-OFF configurations?
In each case, construct compound wffs \(P\) and \(Q\) so that the given statement is a tautology.a. \(P \wedge Q\)b. \(P \rightarrow P^{\prime}\)c. \(P \wedge\left(Q \rightarrow P^{\prime}\right)\)
From the truth table for \(A \vee B\), the value of \(A \vee B\) is true if \(A\) is true, if \(B\) is true, or if both are true. This use of the word "or," where the result is true if both components are true, is called the inclusive or. It is the inclusive or that is understood in the sentence,
Prove that \(A \oplus B \leftrightarrow(A \leftrightarrow B)^{\prime}\) is a tautology. Explain why this makes sense.
Every compound statement is equivalent to a statement using only the connectives of conjunction and negation. To see this, we need to find equivalent wffs for \(A \vee B\) and for \(A \rightarrow B\) that use only \(\wedge\) and '. These new statements can replace, respectively, any occurrences of
Show that every compound wff is equivalent to a wff using only the connectives of \(\vee\) and '.Exercises 47-50 show that defining four basic logical connectives (conjunction, disjunction, implication, and negation) is a convenience rather than a necessity because certain pairs of connectives are
Show that every compound wff is equivalent to a wff using only the connectives of \(\rightarrow\) and '.Exercises 47-50 show that defining four basic logical connectives (conjunction, disjunction, implication, and negation) is a convenience rather than a necessity because certain pairs of
Prove that there are compound statements that are not equivalent to any statement using only the connectives \(\rightarrow\) and \(\vee\).Exercises 47-50 show that defining four basic logical connectives (conjunction, disjunction, implication, and negation) is a convenience rather than a necessity
The binary connective \(\mid\) is called the Sheffer stroke, named for the American logic professor Henry Sheffer, who proved in 1913 that this single connective is the only one needed. The truth table for \(\mid\) is given here. Sheffer also coined the term "Boolean algebra," the topic of Chapter
The binary connective \(\downarrow\) is called the Peirce arrow, named for American philosopher Charles Peirce (not for the antique automobile). The truth table for \(\downarrow\) is given here. In Chapter 8 we will see that this truth table represents the NOR gateShow that every compound statement
Propositional wffs and truth tables belong to a system of two-valued logic because everything has one of two values, False or True. Three-valued logic allows a third value of Null or "unknown" (Section 5.3 discusses the implications of three-valued logic on databases). The truth tables for this
Propositional wffs and truth tables belong to a system of two-valued logic because everything has one of two values, \(\mathrm{F}\) or \(\mathrm{T}\), which we can think of as 0 or 1 . In fuzzy logic, or many-valued logic, statement letters are assigned values in a range between 0 and 1 to reflect
In a three-valued logic system as described in Exercise 53, how many rows are needed for a truth table with \(n\) statement letters?
In 2003, then U.S. Secretary of Defense Donald Rumsfeld won Britain's Plain English Campaign 2003 Golden Bull Award for this statement: "Reports that say that something hasn't happened are always interesting to me, because as we know, there are known knowns, there are things we know we know. We
Four machines, \(A, B, C\), and \(D\), are connected on a computer network. It is feared that a computer virus may have infected the network. Your security team makes the following statements:a. If \(D\) is infected, then so is \(C\).b. If \(C\) is infected, then so is \(A\).c. If \(D\) is clean,
The Dillies have five teenaged children, two boys named Ollie and Rollie, and three girls named Mellie, Nellie, and Pollie. Each is a different number of years old, from 13 to 17. There are three bedrooms for the children in the Dillie house, so two share the yellow room, two share the white room,
An advertisement for a restaurant at an exclusive club in Honolulu says, "Members and nonmembers only." Give two possible interpretations of this statement.
The following newspaper headline was printed during a murder trial:"I am a liar" says murder defendant!Can the jury reach any conclusion from this statement?
You meet two of the inhabitants of this country, Percival and Llewellyn. Percival says, "At least one of us is a liar." Is Percival a liar or a truth teller? What about Llewellyn? Explain your answer.In Exercises 61-64, you are traveling in a certain country where every inhabitant is either a
Traveling on, you meet Merlin and Meredith. Merlin says, "If I am a truth teller, then Meredith is a truth teller." Is Merlin a liar or a truth teller? What about Meredith? Explain your answer.In Exercises 61-64, you are traveling in a certain country where every inhabitant is either a truthteller
Next, you meet Rothwold and Grymlin. Rothwold says, "Either I am a liar or Grymlin is a truth teller." Is Rothwold a liar or a truth teller? What about Grymlin? Explain your answer.In Exercises 61-64, you are traveling in a certain country where every inhabitant is either a truthteller who always
Finally, you meet Gwendolyn and Merrilaine. Gwendolin says, "I am a liar but Merrilaine is not." Is Gwendolyn a liar or a truth teller? What about Merrilaine?In Exercises 61-64, you are traveling in a certain country where every inhabitant is either a truthteller who always tells the truth or a

Mathematical Structures For Computer Science Discrete Mathematics And Its Applications 7th Edition Judith L. Gersting - Solutions

Step by Step Answers