Solve Problem 10-38 using the Goodman-Zimmerli fatigue-failure criterion. 

Data in Problem 10-38

Design the spring of Example 10-5 using the Gerber-Zimmerli fatigue-failure criterion.

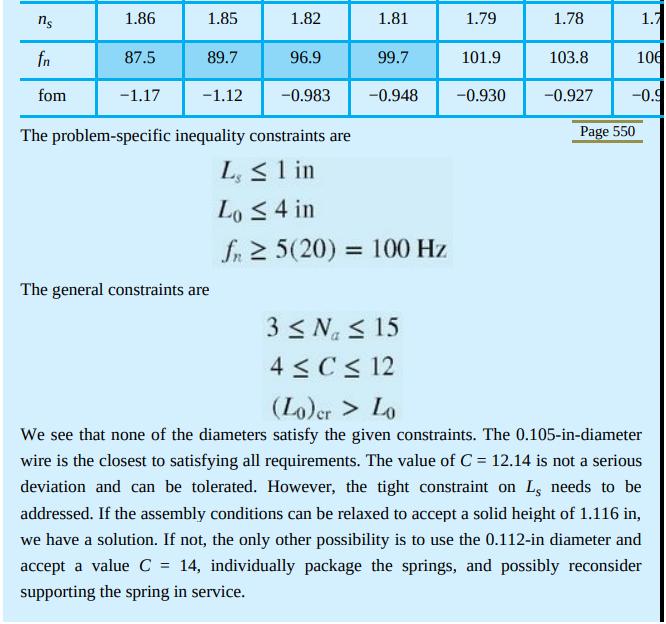
EXAMPLE 10-5 A music wire helical compression spring with infinite life is needed to resist a dynamic load that varies from 5 to 20 lbf at 5 Hz while the end deflection varies from to 2 in. Because of assembly considerations, the solid height cannot exceed 1 in and the free length cannot be more than 4 in. The springmaker has the following wire sizes in stock: 0.069, 0.071, 0.080, 0.085, 0.090, 0.095, 0.105, and 0.112 in. Solution The a priori decisions are: Material and condition: for music wire, A = 201 kpsi in", m = 0.145, G = 11.75(106) psi; relative cost is 2.6 Surface treatment: unpeened End treatment: squared and ground Robust linearity: } = 0.15 Set: use in as-wound condition Fatigue-safe: nf = 1.5 using the Sines-Zimmerli fatigue-failure criterion Function: Fmin = 5 lbf, Fmax = 20 lbf, ymin = 0.5 in, ymax = 2 in, spring operates free (no rod or hole) Decision variable: wire size d The figure of merit will be the cost of wire to wind the spring, Equation (10-22) without density. The design strategy will be to set wire size d, build a table, inspect the table, and choose the satisfactory spring with the highest figure of merit. Set d= 0.112 in. Then a= Fa = B = k = 20-5 2 Sut Fm max ymax -= 7.5 lbf 20 2 = 10 lbf/in Fm = = 23 333 psi 201 = 276.1 kpsi 0.1120.145 Su = 0.67(276.1) = 185.0 kpsi Sy = 0.45(276.1) = 124.2 kpsi From Equation (10-28a), with the Sines criterion, Sse= Ssa = 35 kpsi. Equation (10-23) can be used to determine C with Sse, nf, and Fa in place of Ssy, ns, and (1+)Fmax, respectively. Thus, Sye 35 000 nf 1.5 8Fa 8(7.5) d (0.112) Page 548 = 1522.5 psi 20 +5 2 = 12.5 lbf