A first-order low-pass analog filter has a transfer function  H(s) = 1/(s + 1).

(a) If for this filter, the input is x(t) and the output is y(t) what is the  ordinary differential equation representing this filter.

(b) Suppose that we change this filter into a discrete filter using the  bilinear transformation

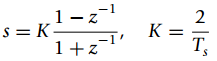
Obtain the transfer function H(z). If for the discrete filter, the  input is x[n] and the output y[n] obtain the difference equation  representing the discrete filter.

(c) Suppose x(t) = u(t) ˆ’ u(t ˆ’ 0.5) find the output of the analog filter.

(d) Let K = 1000, so that T_s = 2/K is used to sample x(t) to get the  discrete signal x[n]. Use the difference equation to solve for the output y[n]. Compare your result with the one obtained by solving the ordinary differential equation for the first three values.

1-z-1 K = -1 T,