Consider the following problems connected with the feedback system shown in Figure 6.23.

(a) The transfer function of the plant in Figure 6.23 is G(s) = 1/(s(s + 1)). If we want the impulse response of the feedback system to be

h(t) = 0.5774e^ˆ’t sin(ˆš3t) u(t)

find the value αin the feedback transfer function F(s) = s + α that would give such impulse response.

(b) In the feedback system shown in Figure 6.23, we know that when there is no feedback (i.e., F(s) = 0), for input x(t) = e^ˆ’t u(t) the output is y(t) = cos(t) u(t).

i. Find G(s) and determine if it corresponds to a BIBO stable plant or not.

ii. Find F(s) so that the output is y(t) = e^ˆ’t u(t) when x(t) = cos(t) u(t), i.e., we reverse the open-loop transfer function.

iii. Is the system with transfer function F(s) BIBO stable?

iv. Find the impulse response h(t) of the overall system. Is the overall system BIBO stable?

Figure 6.23:

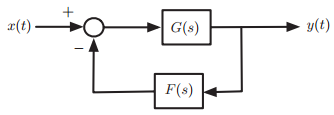
æ(t) – y(t) G(s) F(s)