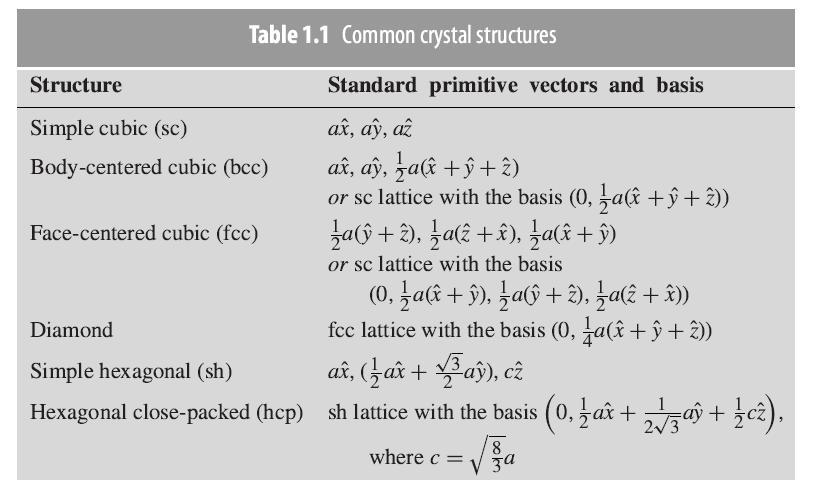
Question: (a) A graphene lattice, or honeycomb lattice, is the same as the graphite lattice (see Table 1.1) but consists of only a two-dimensional sheet with
(a) A graphene lattice, or “honeycomb” lattice, is the same as the graphite lattice (see Table 1.1) but consists of only a two-dimensional sheet with lattice vectors![]()
and a two-atom basis including only the graphite basis vectors in the z = 0 plane. Show that the reciprocal lattice vectors of this lattice are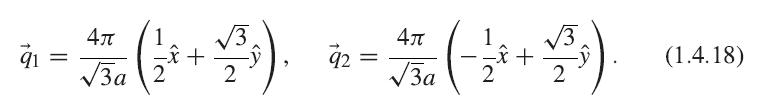
Make a drawing of both the real-space and reciprocal-space lattices, and draw the Brillouin zone on the reciprocal space lattice.
(b) Show that the structure factor for the two-atom basis multiplies the peak in reciprocal space at![]()
and the peak at![]()
Label the reciprocal lattice vectors on your drawing by their peak height and show that the reciprocal lattice has the same symmetry as the real-space honeycomb lattice, and is not a simple hexagonal lattice.
(c) Show that the reciprocal lattice of graphene can be viewed as a simple hexagonal lattice with primitive vectors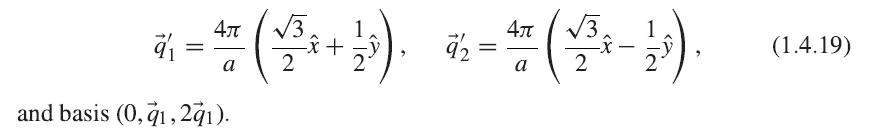
(d) Show that the reciprocal lattice of this reciprocal lattice is a simple hexagonal lattice in real space with primitive vectors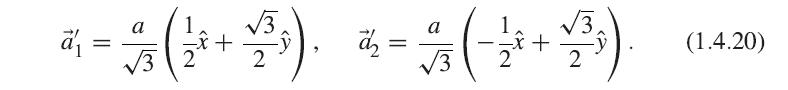
(e) Last, show that the structure factor of the reciprocal lattice in (c) eliminates one of every three real-space lattice points from the lattice of (d), leaving the original honeycomb lattice.


12 a and a
Step by Step Solution
3.43 Rating (156 Votes )
There are 3 Steps involved in it
and using the same volume in the denominator Th... View full answer

Get step-by-step solutions from verified subject matter experts


