Show that for the Hamiltonian H = −(h̄²/2m)∇² + U(r(vector)), an equivalent way of writing (1.9.9) is

where E_n(0) is the unperturbed atomic orbital energy and U₀(r(vector)) is the potential energy function of a single atom. In other words, the band energy depends on the difference of the periodic potential and the single-atom potential.

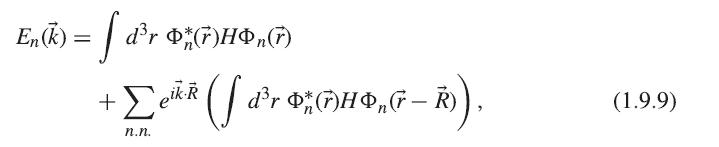
En(k) = En(0) + dr * G7)[UG) Uo(7)]n() + ekR ( [[ r *(7)[UG) Uo(F)]n( R) -R)). - n.n. (1.9.12)