Show that in the case when U(x) = 0 and u k = 1, that is, the states are plane waves = e i(kxt)

Show that in the case when U(x) = 0 and u_k = 1, that is, the states are plane waves ψ = e^i(kx−ωt) in a vacuum, and both k and ω are time-dependent, the solution of (2.8.14) for k = 0 at t = 0 implies k = qEt/h̄ and ω = (qEt)²/6h̄m.

Show that this implies that the average value of the energy, defined by

is equal to h̄²k²/2m. In other words, the kinetic energy grows in time in this case, and there is no Bragg reflection.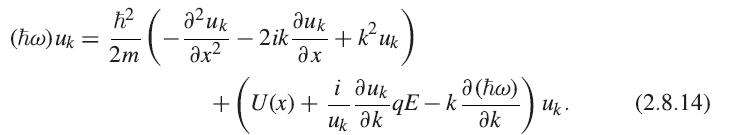

a s H ca s dx *Hy = Jo av dx y* ih- t (2.8.16)