Consider a Young's interference experiment performed with broadband light.

(a) Show that the field incident on the observing screen can be expressed as

\[ \mathbf{u}(Q, t)=\tilde{K}_{1} \frac{d}{d t} \mathbf{u}\left(P_{1}, t-\frac{r_{1}}{c}\right)+\tilde{K}_{2} \frac{d}{d t} \mathbf{u}\left(P_{2}, t-\frac{r_{2}}{c}\right) \]

where

\[ \tilde{K}_{i} \triangleq \iint \frac{\chi\left(\theta_{i}\right)}{2 \pi c r_{i}} d S_{i} \approx \frac{\chi\left(\theta_{i}\right) A_{i}}{2 \pi c r_{i}}, \quad i=1,2 \]

the integral being over the area \(A_{i}\) of the \(i\) th pinhole.

(b) Using the result of part (a), show that the intensity of the light striking the screen can be expressed as

\[ I(Q)=I^{(1)}(Q)+I^{(2)}(Q)-2 \tilde{K}_{1} \tilde{K}_{2} \operatorname{Re}\left\{\frac{\partial^{2}}{\partial \tau^{2}} \boldsymbol{\Gamma}\left(\frac{r_{2}-r_{1}}{c}\right)\right\} \]

where

\[ I^{(i)}(Q)=\tilde{K}_{i}^{2}\left\langle\left|\frac{d}{d t} \mathbf{u}\left(P_{i}, t-\frac{r_{i}}{c}\right)\right|^{2}\rightangle, \quad i=1,2 \]

(c) Show that the preceding expression for \(I(Q)\) reduces to that obtained in Eq. (5.2-10) when the light is narrowband.

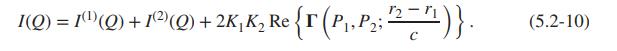
1(Q) = 1()(Q) +1(2)(Q) + 2K, K Re Re {r (P, P2; 1/2 1)}. (5.2-10) C