Question: Let X be a random variable of the continuous type that has pdf f(x). If m is the unique median of the distribution of X

Let X be a random variable of the continuous type that has pdf f(x). If m is the unique median of the distribution of X and b is a real constant, show that

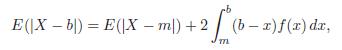
E (X b}) = E(X m)) + 2 [*(b x) (x) dx,

provided that the expectations exist. For what value of b is E(|X −b|) a minimum?

E (X b}) = E(X m)) + 2 [*(b x) (x) dx, - -

Step by Step Solution

★★★★★

3.34 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Given that the median of X is m we can write EXb EXm Emb EXm i... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Statistical Techniques in Business Questions!

Let x be a random variable that represents white blood cell count per cubic milliliter of whole blood. Assume that x has a distribution that is approximately normal, with mean Î¼ = 7500...

Let X be a random variable that takes on nonnegative values and has distribution function F(x). Show that Hint: Integrate by parts. Illustrate this result by calculating E(X) by this method if X has...

Let x be a random variable representing percentage change in neighborhood population in the past few years, and let y be a random variable representing crime rate (crimes per 1000 population). A...

I have three questions shown in the following screenshots Problem 2. Let X1, X2, . . ,Xn be i.i.d. random samples (for example, the times of failure of 12. items) from an exponential distribution...

Let X be a random variable with a continuous distribution such that the interquartile range (IQR) is . Prove that the IQR of aX + b is a for all a > 0 and all b. 12. Let X be a random variable with a...

Let X be a random variable with cumulative distribution function (CDF) given by F X(x) = {1-e^(-3x^(2)), x>=0 and 0, otherwise (a) Find the probability density fuctnion (PDF) of X. (b) Find the mean,...

1. Let X be a random variable and its probability density function (pdf) is f(x) = 0x-1; 0 1. Let X be a random variable and its probability density function (pdf) is f (x) = Oxol; O

Let X be a random variable of the mixed type having the distribution function F (x) = 0 where x

1. Let X be a random variable and its probability density function (pdf) is f(x) = 0x-1; 0 1. Let X be a random variable and its probability density function (pdf) is f (x) = Oxol; O

Use Microsoft Excel to complete all requirements listed below for the following problem, and turn in your Excel file that includes your solutions for all problem requirements. This problem involves...

At what point in time does a company recognize an expense when it uses the allowance method of accounting for uncollectible accounts? When a customers account is identified as being uncollectible At...

2.75 A random sample of 200 adults are classified below by sex and their level of education attained. Education Male Female Elementary 38 45 Secondary 28 50 College 22 17 If a person is picked at...

To what extent is heartbreak real? Reality TV (as distinct from documentaries or other non-fictional TV programmes like sports coverage and news) is a form of television programming that has become...

Suppose two fair dice are tossed. Find the expected value of the product of the faces showing.

Find E(R) for a two-resistor circuit similar to the one described in Example 3.9.2, where fX,Y(x, y) = k(x + y), 10 x 20, 10 y 20.

If a typist averages one misspelling in every 3250 words, what are the chances that a 6000-word report is free of all such errors? Answer the question two ways- first, by using an exact binomial...

Suppose you bought a bond with an annual coupon of 10 percent one year ago for $1,180. The bond sells for $1,235 today. Assuming a $1,000 face value, what was your total dollar return on this...

Alpha Limited discloses its liquidity details: Market securities yeld 12% mnowalhy (assuming 360 days/yr). Transaction cost (b) is 3,600, and daily carh balancess standard deviation (Sigma) is 6,000....

The most recent financial statements for Crosby, Incorporated, follow. Interest expense will remain constant, the tax rate and the dividend payout rate will also remain constant. Costs, other...