Let X' = [X 1 ,X 2 ] be bivariate normal with matrix of means ' = [ 1 , 2 ] and positive

Let X' = [X₁,X₂] be bivariate normal with matrix of means μ' = [μ₁, μ₂] and positive definite covariance matrix Σ. Let

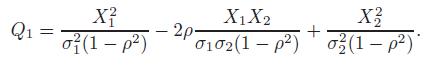
Show that Q₁ is χ2(r, θ) and find r and θ. When and only when does Q₁ have a central chi-square distribution?

Q: X o(1 - p) X1 X2 0102(1-p) - 2p- + X2/ (1 - p)