If T is a continuous random variable that is always positive (such as a waiting time), with probability density function f (t) and cumulative distribution function F(t), then the hazard function is defined to be the function

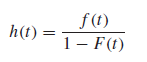
The hazard function is the rate of failure per unit time, expressed as a proportion of the items that have not failed.

a. If T ˆ¼ Weibull (α, β), find h(t).

b. For what values of α is the hazard rate increasing with time? For what values of α is it decreasing?

c. If T has an exponential distribution, show that the hazard function is constant.

f (t) h(t) : 1- F(t)