Let y 1 , y 2 , , y n be a random sample of n observations from an exponential distribution with mean Derive a large sample confidence interval for Start with the pivotal statistic and show that for large samples, Z is approximately a standard normal random variable Then substitute y for in the denominator (why can you do this ) and follow the pivotal method of Example 7 6 y B Z B Vn

Question: Let y 1 , y 2 , . . . , y n be a random sample of n observations from an exponential distribution with

Let y₁, y₂, . . . , y_n be a random sample of n observations from an exponential distribution with mean β. Derive a large-sample confidence interval for β. Start with the pivotal statistic

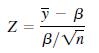
y - B Z = B/Vn

and show that for large samples, Z is approximately a standard normal random variable. Then substitute y̅ for β in the denominator (why can you do this?) and follow the pivotal method of Example 7.6.

y - B Z = B/Vn

Step by Step Solution

★★★★★

3.41 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To derive a confidence interval for we start by defining the pivotal statistic Z y n where y is the ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineering And The Sciences Questions!

In taking a sample of n observations from a population of N members, the variance of the sampling distribution of the sample means is as follows: They quantity (N - n) / (N - 1) is called the finite...

Let X1, X2, X3 be a random sample of size n = 3 from the exponential distribution with pdf f(x) = ex, 0

Let X1, X2, X3 be a random sample of size n = 3 from an exponential distribution with mean > 0. Reject the simple null hypothesis H0: = 2, and accept the composite alternative hypothesis H1:

Hi, it's me again Thanks for helping me with the answer last time d u 1. (a) Let Y1, Y2, ..., Yn be a random sample from a Bernoulli (p) distribution (i.e. Binomial(1, p)). Show ELI K is a minimal...

STA5326 - Mathematical Statistics - II Homework # 3 1. If X 1 , X 2 ,..., X n is a random sample of size n from N ( , 2 ), , show that n n n 2 2 X j , X j or X , X j = = j 1 j 1 =j 1 is a sufficient...

\f 1 Let X 1 , X 2 ,....., X n is a random sample from a normal distribution with mean and variance 02 known. Then probabilily density function 1 x i 2 0 1 f xi 2 e , xi , 0, 0 2 By def, Likelihood...

Q6. Suppose that X =61 + 52, where 1 N N(6,1), 52 ~ N()\\6', A2), and 1 and 52 are in- dependent. Here, A 2 1 is a given constant, and 6 is a unknown parameter. (iv) Let X 1, X 2, - - - ,Xn be an...

1. Let q; > 0 be a population parameter, and let X l , X 2, , X n be a random sample from a distribution with probability density function 2 105311) : 2 9K A, , x> 0. zero otherwise. m Recall: W = X2...

Recall: k) In addition to many other wonderful services it provides, CourseCheggHero benets nancially from its customers' inability and/ or unwillingness to do their homework. Suppose that the time...

11/26/2016 Fall 2016 Homework 12Due Thursday 12/1, before 8 PM. Must submit before 8PM. My sites / 16F-STATS100A-1 / HOMEWORK / Fall 2016- Homework 12-Due Thursday 12/1, before 8 PM. Must submit...

Effective control of insulin injections can result in better lives for diabetic persons. Automatically controlled insulin injection by means of a pump and a sensor that measures blood sugar can be...

What is meant by the best-fitting line? Is the best-fitting line necessarily a good-fitting line? Explain.

XYZ Company has a net loss of $ 1 0 0 , 0 0 0 for the year and pays dividends of $ 3 0 , 0 0 0 to its shareholders. How will this impact Retained Earnings? Retained earnings will decrease by $ 7 0 ,...

4. When doctors communicate with technical language, they are using a. profanity b. euphemisms c. doublespeak d. jargon

56. For any events A and B with P(B) 0, show that P(AB) P(A B) 1.

57. If P(BA) P(B), show that P(B A) P(B ). [Hint: Add P(B A) to both sides of the given inequality and then use the result of Exercise 56.]

58. Show that for any three events A, B, and C with P(C) 0, P(A BC) P(AC) P(BC) P(A BC).

Help with finding the probability The table summarizes results from 983 pedestrian deaths that were caused by automobile accidents. Pedestrian Deaths Driver Pedestrian Intoxicated? Intoxicated? Yes...

SPSS 5.2 - T Tests SCENARIO # 1 Previous research indicates that children born by diabetic mothers may suffer from high blood pressure, among other health problems. A group of researchers collected...

Hyperion Inc., currently sells its latest high-speed colour printer, the Hyper 500, for $333. Its cost of goods sold for the Hyper 500 is $190 per unit, and this year's sales (at the current price of...