Question: Let y 1 , y 2 , . . . , y n denote a random sample from a uniform distribution with probability density a.

Let y1, y2, . . . , yn denote a random sample from a uniform distribution with probability density

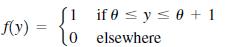
[1 if e s ys 0 + 1 0 elsewhere

a. Show that y̅ is a biased estimator of θ, and compute the bias.
b. Find V(y̅).
c. What function of y̅ is an unbiased estimator of θ?    

[1 if e s ys 0 + 1 0 elsewhere

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

To determine whether y the sample mean is a biased estimator of the population mean we need to calcu... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineering And The Sciences Questions!

Q:

Let X1, X2, .. , X7 denote a random sample from a population having mean and variance. Consider the following estimators of μ: (a) Is either estimator unbiased? (b) Which estimator is best? In...

Q:

Let X1,..., Xn be a random sample from a uniform distribution on the interval (, 2), > 0. Find a minimal sufficient statistic for . Is the statistic complete?

Q:

Let X1, X2, X3 denote a random sample of size n = 3 from a distribution with the geometric pmf (a) Compute P(X1 = 1, X2 = 3, X3 = 1). (b) Determine P(X1 + X2 + X3 = 5). (c) If Y equals the maximum of...

Q:

Hi, it's me again Thanks for helping me with the answer last time d u 1. (a) Let Y1, Y2, ..., Yn be a random sample from a Bernoulli (p) distribution (i.e. Binomial(1, p)). Show ELI K is a minimal...

Q:

\f 1 Let X 1 , X 2 ,....., X n is a random sample from a normal distribution with mean and variance 02 known. Then probabilily density function 1 x i 2 0 1 f xi 2 e , xi , 0, 0 2 By def, Likelihood...

Q:

Recall: k) In addition to many other wonderful services it provides, CourseCheggHero benets nancially from its customers' inability and/ or unwillingness to do their homework. Suppose that the time...

Q:

need full answer to attached question 3. Let X 1, X 2, . . . , X n be a random sample from a population with probability density function (26 i 1) 6 1 7 I9 fx(59;9) = (:6) 5'3 Find a Maximum...

Q:

I would like to get the help from Question 1-12 Thanks for helping Directions: Submit solutions to the following problems in beginning of lecture on the due date. Make sure that your solutions are...

Q:

11/26/2016 Fall 2016 Homework 12Due Thursday 12/1, before 8 PM. Must submit before 8PM. My sites / 16F-STATS100A-1 / HOMEWORK / Fall 2016- Homework 12-Due Thursday 12/1, before 8 PM. Must submit...

Q:

please show full working and explanations. 5. (10 marks) Let Y, . . ., Y,, denote a random sample from the probability density function f (3; 0) - - exp _(logy/)? ] for y > 0 and 0 > 0 20 and f(y; 0)...

Q:

Suppose you are considering investing an equal proportion of your wealth in two stocks. Stock C offers a 15% return while stock T offers a 25% return assuming a boom economy occurs for which there is...

Q:

Consider the following quasi-linear PDE, x Ju t where the initial condition is + (1+2u) =-u; f (x) = 1. |x|>1 x 1 (2) - {- = 2x, u (x,0) = f (x) 1, 2+x, 2 - x, 1, x 1 (8)

Q:

The mortgage amount borrowed divided by the initial purchase price is its Group of answer choices value - to - loan ratio. price - to - rent ratio. loan - to - value ratio. debt - to - equity ratio.

Q:

4. What are the three main stages of social media video production and why are each important?

Q:

71. An oil exploration company currently has two active projects, one in Asia and the other in Europe. Let A be the event that the Asian project is successful and B be the event that the European...

Q:

72. In Exercise 13, is any Ai independent of any other Aj? Answer using the multiplication property for independent events.

Q:

73. If A and B are independent events, show that A and B are also independent. [Hint: First establish a relationship between , P(B), and .]

Q:

The following table gives abbreviated balance sheets and income statements for Este Lauder Companies Assume a corporate tax rate of 33.57%. $ in millions) End of Year Start of Year Balance Sheet...

Q:

7 Consider the table given below to answer the first question (shares and market values in milions). Claway Gol (KIT) Alaska ir Group (ALE) Entergy (BR) Yunt tranda (YUX) General Electric (GE) 12.5...

Q:

An annual coupon bond has a face value of $1,000 and a coupon rate of 6.0%. Time to maturity is 16 years and the current yield to maturity is 7.5%. What percentage of this bond's value is due to its...