Refer to Exercise 14.8. Use Bonferroni’s method to compare the mean heat rates of the three gas turbine engines. Use α = .06.

Data from Exercise 14.8

Refer to the Journal of Engineering for Gas Turbines and Power (Jan. 2005) study of gas turbines augmented with high-pressure inlet fogging, Exercise 8.39. Recall that the researchers classified gas turbines into three categories—traditional, advanced, and aero derivative—and measured the heat rate (kilojoules per kilowatt per hour) of sampled gas turbines of each type. The data in the GASTURBINE file was analyzed using a completely randomized design ANOVA; the results are shown in the MINITAB printout below.

Data from Exercise 8.39

Refer to the Journal of Engineering for Gas Turbines and Power (Jan. 2005) study of gas turbines augmented with high-pressure inlet fogging, Exercise 8.29. The researchers classified gas turbines into three categories: traditional, advanced, and aero derivative. Summary statistics on heat rate (kilojoules per kilowatt per hour) for each of the three types of gas turbines in the sample are shown in the MINITAB printout.

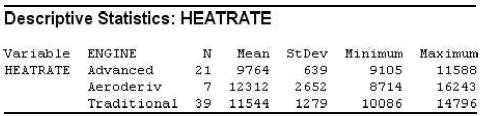
Data from Exercise 8.29

During periods of high electricity demand, especially during the hot summer months, the power output from a gas turbine engine can drop dramatically. One way to counter this drop in power is by cooling the inlet air to the gas turbine. An increasingly popular cooling method uses high-pressure inlet fogging. The performance of a sample of 67 gas turbines augmented with high-pressure inlet fogging was investigated in the Journal of Engineering for Gas Turbines and Power (Jan. 2005). One measure of performance is heat rate (kilojoules per kilowatt per hour). Heat rates for the 67 gas turbines are listed in the table on the bottom of page. Suppose that a standard gas turbine has, on average, a heat rate of 10,000 kJ/kWh. Conduct a test to determine if the mean heat rate of gas turbines augmented with high-pressure inlet fogging exceeds 10,000 kJ/kWh. Use α = .10.

Transcribed Image Text:

One-way ANOVA: HEATRATE versus ENGINE Source DF MS F P ENGINE 2 553 60022 27680011 15.74 0.000 Error 64 112537186 1758394 Total 66 167897208 3 = 1326 R-Sq = 32.97% R-3q (ad)) - 30.88% Individual 95% CIs For Mean Based on Pooled StDev Level IN Mean StDev ---+---- Advanced 21 9764 639 ( オー-ーー) deroderiv 7 123 12 2652 Traditional 39 11544 1279 (--オーーー) --- 9600 10800 12000 13200 Ponled St.Dev = 132.6