Consider two independent samples from normal populations having the same variance 2, of respective sizes n and m. That is, X1, . . . ,

Consider two independent samples from normal populations having the same variance σ2, of respective sizes n and m. That is, X1, . . . , Xn and Y1, . . . , Ym are independent samples from normal populations each having variance σ2. Let S2 x

and S2 y denote the respective sample variances. Thus both S2 x and S2 y are unbiased estimators of σ2. Show by using the results of Example 7.7b along with the fact that Var(χ2 k) = 2k where χ2 k is chi-square with k degrees of freedom, that the minimum mean square estimator of σ2 of the form λS2 x

+ (1 − λ)S2 y is

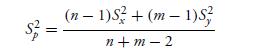
This is called the pooled estimator of σ2.

(n-1)+(m1)S n+m-2