Let X be a Poisson random variable with parameter 0, that is, with probability mass function

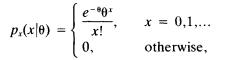
where 0 > 0, and let the loss function L(0,8) = (0 - 8)2/0.

(a) Show that the maximum-likelihood estimator 80 = A" of 0 is an equalizer decision rule.

(b) Find the Bayes decision rule with respect to the prior density n(0),

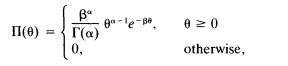
which is a gamma G (a,p) with parameters (a,p).

(c) Show that 80 is extended Bayes and hence minimax.

(d) Show that 80 is admissible.

e-g -80x P.(x|0) x = 0,1,... 0, x! otherwise,