Question: Let ( X UX 2) follow a bivariate normal distribution with E ( X 0 = E ( X 2) = 0, V(X x) =

Let ( X UX 2) follow a bivariate normal distribution with E ( X 0 = E ( X 2) = 0, V(X x) = V(X2) = 1.

Let the coefficient of correlation between X x and X 2 be equal to p.

Find the distribution of Y2 — Y u where Y2 = max(XuX 2), Y x = m i n ^ , ^ ) .

Calculate the probability P{Y2 > 0}. Show that

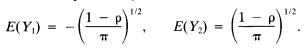
E(Y) = -(1-9)". E(Y) = = (1 = 9)". 1/2

E(Y) = -(1-9)". E(Y) = = (1 = 9)". 1/2

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineers And Scientists Questions!

Q:

2 - 4 1 . Determine the components of reaction at the pinned supports A and C of the two - member frame. Neglect the thickness of the members. Assume B is a pin. Prob. 2 - 4 1

Q:

Please resolve. Jack and Sam are both taking a statistics class this summer. They decided to study separately for their exam. The probability that Jack will make an "A" in statistics is 0.6, and the...

Q:

Answer the following questions: a. Let X and Y follow the bivariate normal distribution with parameters , 2, 01, 02, p. Show that W = X- and Q = (Y) - p2(X-) are independent normal random variables....

Q:

Problem 5.67 Let the random vector (X, Y ) have the joint density function f(x, y) = xexyx, for x > 0,y> 0) f(x, y)=0, elsewhere. Compute: (a) f(y|x). (b) Y |x. Problem 5.68 Let X and Y have a...

Q:

Let x and y have a bivariate normal distribution and suppose that x and y both have mean 0 and variance 1, so that their marginal distributions arc standard normal and their joint density is Show...

Q:

Problem 5.70 Let X and Y have a bivariate normal distribution with parameters X = 2, Y = 1, 2 X = 9, 2 Y = 16, = 3/4. Compute: (a) P(Y

Q:

64. (i) If the joint distribution of X and Y is the bivariate normal distribution (70), then the conditional distribution of Y given X is the normal distribution with variance T2 (1 - p2) and mean...

Q:

(i) If the joint distribution of X and Y is the bivariate normal distribution (5.69), then the conditional distribution of Y given x is the normal distribution with variance 2(1 2) and mean +...

Q:

Attach workings please. Please use R studio, Thank you. 2. The probability of a student passing statistics is known to be 0.41; and the probability of a student passing chemistry is known to be 0.55....

Q:

HO 3. Let X ~ N 2 and (a) Determine the distribution of Y - X. (b) Determine the distribution of Y2|Y1 = y1. 4. Consider X ~ N3(u, E) where X2|X1 = x1 ~ N(-21, 1) E(X1|X2 = 12) = -(12+1)/2 X3|X1 =...

Q:

Solve attached? I need this paper analyzed using qualitative analysis and answer the following questions: Our problem statement was: The problem to be addressed by this assessment is the impact of...

Q:

Paragon Products plc has a factory which manufactures a wide range of plastic household utensils. One of these is a plastic brush which is made from a special raw material used only for this purpose....

Q:

The Athletic Director and Coach of the womens softball team at a large public university are trying to decide to which of these two players they will offer an athletic scholarship (i.e., an...

Q:

The following information relates to Perry Somer s financial affairs in 2 0 2 4 . Perry is employed as a salesperson and is remunerated by commissions. He must pay all of his own expenses. During the...

Q:

a. The United States Congress is well qualified to debate and set generally accepted accounting principles. Comment. b. Speculate on why these bills were directed to amend the Securities Exchange Act...