Probit regression. Consider a probit regression model for a binary response yi on covariates xi

, i = 1, . . . , n. Let Φ(·) denote the standard normal c.d.f.

where β = (β0, β1, β2) and xi = (1, xi1, xi2). We observe the following data.17 These are historical data – do you recognize them?

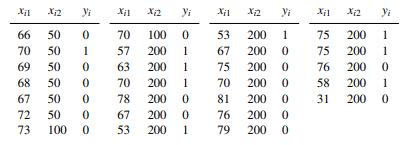
Let y = (y1, . . . , yn) denote the observed data. Assuming an improper prior h(β) = 1, find the marginal posterior distributions h(βj | y), j = 0, 1, 2 and plot the posterior predictive probability p(yn+1 = 1 | y, xn+1) as a function of xn+1.
Start by introducing latent scores zi to replace (6.14) by yi = I(zi > 0) and zi ∼ N(x 0 i β, 1). (6.15)
Here, I(A) is the indicator function of event A. Then,

a. Show that (6.15) is equivalent to (6.14).

b. Find the conditional posterior h(zi | β, y) and h(β | z, y).

c. Propose a Gibbs sampling scheme to simulate from the posterior distribution h(β,z | y).

d. Plot a histogram of simulated β values as an estimate of h(βj | y).

e. Show that E{h(βj | y,z)} = h(βj | y). With respect to which distribution is the expectation?

f. Use

(e) to produce estimates of h(βj | y).
g. Argue why the estimate in

(f) is “better” than (d). How do you formalize “better”?
h. Plot P(yn+1 = 1 | xn+1, y).
Fix xn+1,2 = 100 and plot the posterior predictive probability P(yn+1 = 1 |
xn+1, y) for a grid of values for xn+1,1, say 30

P(y; 1x) (x).