Question: (Symmetric normal distribution) The random vector X = ( X u ...,Xp) f is said to have a symmetric normal distribution if it is distributed

(Symmetric normal distribution) The random vector X = ( X u ...,Xp) f is said to have a symmetric normal distribution if it is distributed as Np(p-,2), where p. = (p-i and

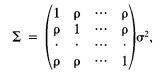
|| p P a. 1 PP P

that is, var(A",) = cr2, cov(Xi,Xj) = pa2 for all i 7^ j = 1 Let 0 be an orthogonal p x p matrix and be defined by

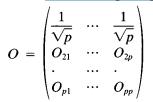
image text in transcribed

and let ’y = (Yu- ~,YP)' = OX. Find F(Y ), cov(Y) and show Y U...,YP are independent.

|| p P a. 1 PP P

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineers And Scientists Questions!

Q:

Suppose that X = (X1, ..., Xp) ~ Np (Mpx1, Epxp) is a random vector and Amxp is a non-random matrix. (a) [3 marks] What is the distribution of Y = AX? (Specify the distribution, its mean and...

Q:

1.) What is the hypothetical likelihood that a considerably number will be moved on a number 3D shape? 2.) What was the test likelihood of how often a much number was really moved utilizing the...

Q:

Table of z values and probabilities for the standard normal distribution. z is the first column plus the top row. Each cell shows P( X z). For example P( X 1.04) = .8508. For z

Q:

Describe, in outline, each of the implicit surface, NURBS surface, and constructive solid geometry methods for defining three-dimensional shapes. (b) Compare and contrast the three methods. (a)...

Q:

Question 2. [26 marks] (a) [6 marks] Consider a p-dimensional random vector X where X-Np(0px1, [pxp). Answer the follow questions. (i) What is the distribution of X1 - 2X2, where X] and X2 are both...

Q:

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Q:

An important problem in multivariate analysis is the test of sphericity of the data, that is, the null hypothesis Ho : ) =021, where of is unspecified. This hypothesis expresses the fact that the...

Q:

Miller-Rabin test to check whether a number N is composite. This will involve computing a N1 mod N for some value of a. [10 marks] Carry out the steps for N = 65 and a = 1, 2, 8 and 12. on what each...

Q:

Helpful hint: The following topics/concepts are covered in this homework, in no particular order (different problems cover different concepts): Class 6: Discrete Probability Distributions The...

Q:

Find the area of the indicated region under the standard normal curve. Click here to view page 1 of the standard normal table. Click here to view page 2 of the standard normal table. ,o,9 E The area...

Q:

Currently, the dividend-payout ratio (D/E) for the aggregate market is 60 percent, the required return (k) is 11 percent, and the expected growth rate for dividends (g) is 5 percent. a. Compute the...

Q:

Choose any islamic bank financial statement Calculate (showing calculations): 1. Return on Equity 2. Return on Assets 3. Cost to Income 4. Gross impaired financing 5. Financing loss coverage ratio 6....

Q:

Marcus inherited 5 0 0 shares of a renewable energy company ( REC ) which had a price of CAD 7 6 exactly four months ago. The price of REC has subsequently declined to CAD 5 2 . Marcus has stated...

Q:

a. Financial statements should aid the user of the statements in making decisions. In your opinion, would the user of the statements be aided if there were a distinction between financial reporting...