The line spread function of a two-dimensional imaging system is defined to be the response of that system to a one-dimensional delta function passing through the origin of the input plane.

(a) In the case of a line excitation lying along the \(x\)-axis, show that the line spread function \(l\) and the point spread function \(p\) are related by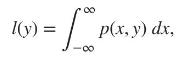

where \(l\) and \(p\) are to be interpreted as amplitudes or intensities, depending on whether the system is coherent or incoherent, respectively.

(b) Show that for a line source oriented along the \(x\)-axis, the (1D) Fourier transform of the line spread function is equal to a slice through the (2D) Fourier transform of the point-spread function, the slice being along the \(f_{y}\)-axis. In other words, if the Fourier transform of \(l\) is \(\widehat{L}\) and the Fourier transform of \(p\) is \(\widehat{P}\), then \(\widehat{L}(f)=\) \(\widehat{P}(0, f)\).

(c) Find the relationship between the line spread function and the step response of the system, that is, the response to a unit step excitation oriented parallel to the \(x\)-axis.

l(y) = = 8 p(x, y) dx,