A compensator for a heat exchange control system is given by

\[D(s)=\frac{10 s+20}{0.1 s+0.5}\]

(a) Use the Matched Pole Zero (MPZ) method to design an equivalent digital compensator \(D(z)\). Use a sampling time of 1 second.

(b) What is the Modified Matched Pole Zero (MMPZ) method? What is its advantage? What is its drawback?

(c) For the same continuous-time compensator \(D(s)\), use the Tustin approximation method to design a digital compensator \(D(z)\). Use a sampling time of 1 second.

(d) Compare the two compensators obtained in

(a) and (c).

(e) If we use a much lower sampling time, say 0.01 seconds, what will happen to the performance of the two compensators? Why is this the case?

(f) What is the critical limitation of digital approximation methods? Describe the direct discrete design of digital systems.

Transcribed Image Text:

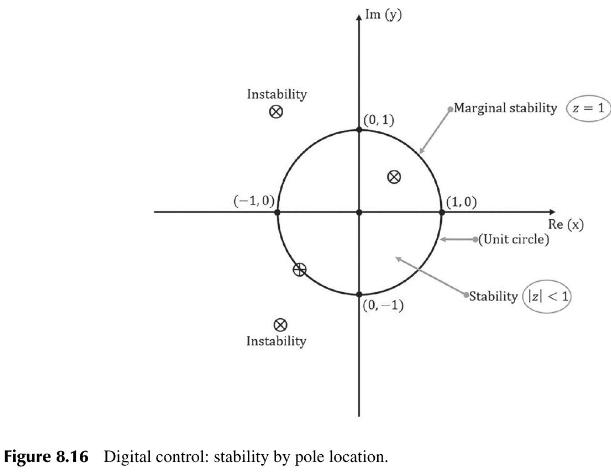
Im (y) Instability Marginal stability (z=1) (0, 1) (-1,0) (1.0) Re (x) (Unit circle) Stability (z <1) (0,-1) Instability Figure 8.16 Digital control: stability by pole location.