Question: A dynamic system is described by the following State-Variable Matrix model such that: (dot{mathbf{x}}=mathbf{A x}) and (mathbf{y}=mathbf{C x}), where (a) Obtain the State-Transition Matrix (Phi(mathbf{t})).
A dynamic system is described by the following State-Variable Matrix model such that: \(\dot{\mathbf{x}}=\mathbf{A x}\) and \(\mathbf{y}=\mathbf{C x}\), where
![0 1 - A= C=3 -1] 0 -2 and x(0) = [12].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1710/3/9/1/34865f28034e5a7e1710391348879.jpg)
(a) Obtain the State-Transition Matrix \(\Phi(\mathbf{t})\).
(b) Find the state variable responses \(x_{1}(t)\) and \(x_{2}(t)\).
(c) Find the output response \(y(t)\).
(d) For this system verify that
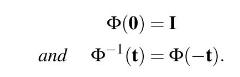
0 1 - A= C=3 -1] 0 -2 and x(0) = [12].
Step by Step Solution
3.46 Rating (162 Votes )
There are 3 Steps involved in it
a The StateTransition Matrix is obtained as follows PhimathbftmathbfeA talphao mathbfIalpha1 mathbfA where alphao and alpha1 are constants obtained fr... View full answer

Get step-by-step solutions from verified subject matter experts


