Consider a dynamic system whose plant transfer function and proportional controller are given (respectively) by

\[\begin{aligned}G(s) & =\frac{1}{20 s} \\D(s) & =K=40\end{aligned}\]

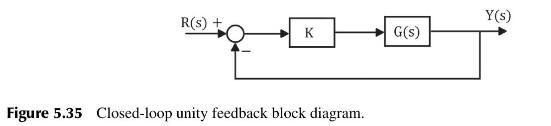
The plant is in a unity feedback arrangement with the proportional controller $K$ as depicted in Figure 5.35.

(a) If the plant is delayed by two seconds, draw the new block diagram.

(b) Find the exact Transfer Function model of the delayed system.

(c) Using the first-order Pade approximation, find the approximate Transfer Function model of the system.

(d) Hence, determine whether the delayed system is stable.

(e) Use MATLAB to draw the root locus of the delayed system using the exact Transfer Function model (where the Pade approximation is implemented in MATLAB). Then use MATLAB to draw the root locus using the hand-calculated approximate Transfer Function model. Compare the two results.

R(s) + Y(s) K G(s) Figure 5.35 Closed-loop unity feedback block diagram.