Question: Consider the following Transfer Function models for three dynamic systems. (a) [H_{1}(s)=frac{5 s}{s^{2}+2 s+5}] (b) [H_{2}(s)=frac{5}{s^{2}+2 s+5}] (c) [H_{3}(s)=frac{omega_{n}^{2}}{s^{2}+2 xi omega_{n}+omega_{n}^{2}}] Find the output for
Consider the following Transfer Function models for three dynamic systems.
(a)
\[H_{1}(s)=\frac{5 s}{s^{2}+2 s+5}\]
(b)
\[H_{2}(s)=\frac{5}{s^{2}+2 s+5}\]
(c)
\[H_{3}(s)=\frac{\omega_{n}^{2}}{s^{2}+2 \xi \omega_{n}+\omega_{n}^{2}}\]
Find the output for each system if the input is a sawtooth signal as shown in Figure 3.41.
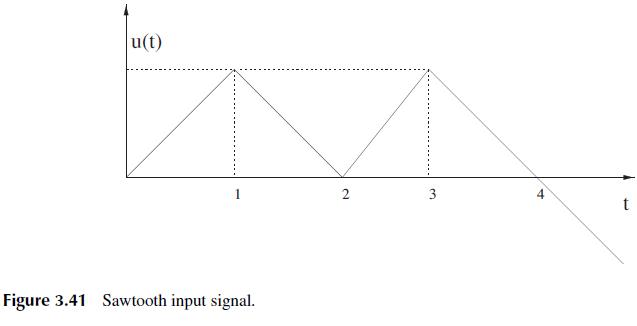
u(t) Figure 3.41 Sawtooth input signal. 2 3 4
Step by Step Solution
3.34 Rating (151 Votes )
There are 3 Steps involved in it
a The sawtooth input signal can be written in the form of a ramp function and a delayed ramp function using superposition principle as follows utrt2 rt12 rt22 rt3 where rtt is the ramp function Thus o... View full answer

Get step-by-step solutions from verified subject matter experts


