Consider the system shown in Figure 5.121, in which a mass-spring system is hung from the middle of a massless beam. Assume that the beam can be modeled as a spring and the equivalent stiffness at the mid-span is \(192 E I_{A} / L^{3}\), where \(E\) is the modulus of elasticity of beam material and \(I_{\mathrm{A}}\) is the area moment of inertia about the beam's longitudinal axis.

a. Derive the differential equation of motion for the system.

b. Using the differential equation obtained in Part (a), determine the transfer function \(X(s) / F(s)\). Assume that the initial conditions are \(x(0)=0\) and \(\dot{x}(0)=0\).

c. Using the differential equation obtained in Part (a), determine the state-space representation. Assume that the output is the displacement \(x\) of the mass.

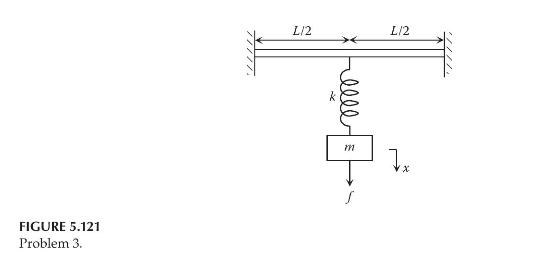
FIGURE 5.121 Problem 3. L/2 L/2 Helll = x