Consider a cylindrical rod of diameter \(d\) undergoing thermal processing and moving at a speed \(u\) as shown below:

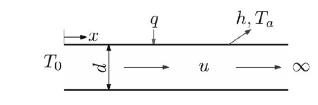
The rod may be assumed to be infinite in the direction of motion. Energy transfer occurs at the outer surface, with a constant heat flux input \(q\) and convective loss to the ambient at temperature \(T_{a}\) and heat transfer coefficient \(h\). Assuming 2-D and steady transport, the governing equation and boundary conditions for the problem are given as

\[
ho C U A \frac{\partial T}{\partial x}=k A\left(\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial T}{\partial r}ight)+\frac{\partial^{2} T}{\partial x^{2}}ight)
\]

The boundary conditions are

\[
\text { at } x=0, T=T_{\infty} ; \quad \text { at } r=0, \frac{\partial T}{\partial r}=0 ; \quad \text { at } r=d / 2, k \frac{\partial T}{\partial r}=q-h\left(T-T_{a}ight)
\]

Use the non-dimensional variable as \[
X=\frac{x}{d}, \quad R=\frac{r}{d}, \quad \theta=\frac{T-T_{a}}{T_{0}-T_{a}}
\]
Find out the relevant non-dimensional parameters using non-dimensionalization of governing equation and boundary condition.

To T P 9 U h, Ta