In the rotational mechanical system shown in Fig. 1.7, determine the transfer function of \(\frac{\theta_{2}(s)}{T(s)}\).

1) \(\frac{J_{1} s^{2}+k}{s^{2}\left(J_{1} J_{2} s^{2}+k\left(J_{1}+J_{2}ight)ight)}\)
2) \(\frac{J_{2} s^{2}+k}{s^{2}\left(J_{1} J_{2} s^{2}+k\left(J_{1}+J_{2}ight)ight)}\)
3) \(\frac{k}{s^{2}\left(J_{1} J_{2} s^{2}+k\left(J_{1}+J_{2}ight)ight)}\)
4) \(\frac{k}{J_{1} J_{2} s^{4}+k\left(J_{1}+J_{2}ight) s^{2}+2 k^{2}}\)

Figure 1.7

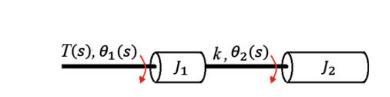
T(s), 0(s), k, 0(s) J1 J2