A quantum particle is restricted to a one dimensional box 0 x L It experiences no forces within the box, but cannot escape At time t 0, the particle is in the state where i (x) are the (correctly normalized) energy basis states from eq (a) Compute the probability at t 0 that the particle has energy E 1 2 2 2mL 2 (b) Compute the probability at t 0 that the particle is in the left half of the box (x (c) Compute the state of the particle at time t What is the probability at this time that the particle has energy E 1 What is the probability that the particle is in the left half of the box VI 3 1 (x) V2 342(x)

Question: A quantum particle is restricted to a one dimensional box 0 ? x ? L. It experiences no forces within the box, but cannot escape.

A quantum particle is restricted to a one dimensional box 0 ? x ? L. It experiences no forces within the box, but cannot escape. At time t = 0, the particle is in the state

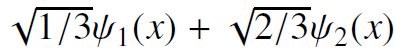
? VI/3 1 (x) + V2/342(x)

where ?_i(x) are the (correctly normalized) energy basis states from eq.?

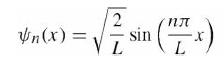
(a) Compute the probability at t = 0 that the particle has energy ? = E₁ = ?²?²/2mL².?

(b) Compute the probability at t = 0 that the particle is in the left half of the box (x

(c) Compute the state of the particle at time t = ??/?. What is the probability at this time that the particle has energy ? = E₁? What is the probability that the particle is in the left half of the box?

VI/3 1 (x) + V2/342(x)

Step by Step Solution

★★★★★

3.45 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a When the state is written as a sum of normalized energy states then the probability of m... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related The Physics Energy Questions!

The wave nature of particles results in the quantum mechanical situation that a particle confined in a box can assume only wavelengths that result in standing waves in the box, with nodes at the box...

(a) Show that, for a particle in a one-dimensional box (Fig. 2.1) of length l, the probability of observing a value of px between p and p + dp is (b) Evaluate (7.112) in terms of (N( for p = ( nh...

Suppose a particle of mass m is confined to a one-dimensional box of width L. According to quantum theory, the particle's wave (with = h/mv) is a standing wave with nodes at the edges of the box....

E-Physics Tutorial Book Note: I have attached below the lesson for the 3 activities. Thank you so much for your time and effort. Activity 1. Directions: Use the right-hand rule to determine the...

Question: 2. Consider a particle in an infinite square well. It is in the initial state y(x, 0) = A [$1(x) + $2(x)] where on (x) is the energy eigenfunctions for the infinite square well. (a) Plot...

I have to do a presentation about Odyssey arts applying Mckinseys 7s framework model to the information given above. identifying any solutions to help them using Mckinseys model please I need help I...

watch the three short clips below then answer the questions Copy and paste the three links below 1) Projectile Motion https://www.nsf.govews/mmg/mmg_disp.jsp?med_id=72205&from= 2) Newton's Second Law...

Commentary Beyond Black Box Epidemiology Douglas L. Weed, MD, PhD "Black box epidemiology" is the most recent addition to a long list of disciplinary subgroups although few practitioners would likely...

please help me solve these questions, the teacher included the final answer in the screenshots but I want the steps for it so I can understand how they got the final answer ( that's all screenshot so...

I would like to do my NFP project onUnited States Fund for United Nations Children's Fund Prepare an executive summary paper on the Form 990 to include the following: a. A brief overview of your...

Partial balance sheet data for Berente Company at December 31, 2014, are as follows: Prepare the Current Assets section of Berente Companys balance sheet at December 31,2014. Finished goods inventory...

Let A be a symmetric positive definite n Ã n matrix. (a) If k where yk Rk and Î²k is a scalar, show that Lk+1 is of the form and determine xk and Î±k in terms of Lk,...

Some factors affecting audit quality are outside the direct control of the auditor, such as the amount of time allotted for completion of the audit. True False

3. The trade-off theory of capital structure predicts that firms have optimal (target) debt ratios. Discuss the differences in the rate of adjustment toward optimal capital structure across countries...

A snowboarder glides down a 50-m-long, 15 o hill. She then glides horizontally for 10 m before reaching a 25 o upward slope. Assume the snow is friction less. a. What is her velocity at the bottom of...

A small child gives a plastic frog a big push at the bottom of a slippery 2.0-m-long, 1.0-m-high ramp, starting it with a speed of 5.0 m/s. What is the frogs speed as it flies off the top of the ramp?

FIGURE EX2.31 shows the acceleration-versus-time graph of a particle moving along the x-axis. Its initial velocity is v 0x = 8.0 m/s at t 0 = 0 s. What is the particles velocity at t = 4.0 s? Figure...

1. (60 pts.) Using the definitions of the hyperbolic functions cosh(x)=21(ex+ex)sinh(x)=21(exex), the basic properties of Laplace transforms, and tables 3.1 and 2.3, find the Laplace transforms,...

The market portfolio ( M ) provides a 1 5 % annual return with a 2 0 % standard deviation. The risk - free rate of return ( r f ) is 5 % per annum. Security Q and P provide 1 7 % and 1 1 % return per...

Assume that the expectations theory fully explains the Treasury Bond Yield Curve. The 10-year zero-coupon bond maturing in 2030 has a yield-to-maturity (YTM) of 3.5%. Assume that instead of simply...