Consider the logistic map Derive analytically an expression for the fixed point x* given by x* = (x*) and the point xtan for which (x)

Consider the logistic map

Derive analytically an expression for the fixed point x* given by x* = ƒ(x*) and the point xtan for which ƒ(x) has a tangent parallel to the identity, i.e. ƒ(xtan) = 1. Use the expression in Eq. (12.40) to estimate the number of iterations needed to pass through the bottleneck.

Equation (12.40)

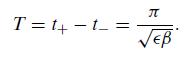
Choose r = 1 + Δ . For Δ = 0.1,0.01 and 0.001, numerically iterate the map and determine the number of iterations, T, needed to go from x(0) = 10⁻⁵  to X(T) = x* ± 10⁻⁵; compare your results with the results obtained from Eq. (12.40).

Equation (12.40)

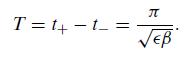
x(t + 1) = f(x(t))] = rx(t)(1 x(t)). -