The deformation in a solid can be described by a vector field u(x) = (u1, u2, u3) describing the displacement of the solid away from the equilibrium point x. This is similar to the displacement vector s used to analyze waves in ?31.2. For small deformations, the strain tensor ? is a 3 ? 3 matrix with elements ?_{i j} = (?u_i/?x_j + ?u_j/?x_i)/2. For example, a rod compressed uniformly to 99% of its original length in the x-direction would have ?₁₁ = ?0.01. The energy of compression is given by eq (33.13)

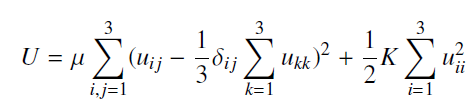
where ? is the shear modulus, K is the bulk modulus, and ?_{i j} = 1 if i = j and 0 otherwise.?

(a) Show that for uniform hydrostatic compression, where u₁₁ = u₂₂ =u33 = u, and all other components vanish, the energy of compression depends only on K.?

(b) Show that for P- wave compression, where u₁₁ = u sin (kx) and all other components vanish, the energy of compression is proportional to the elastic modulus ? = K + 4?/3.?

3 3 3 U =(uij - oij ue)- > Ukk) + 3 k=1 i,j=1 i=1