12. For a Markov chain {Xn, n 0} with transition probabilities Pi,j , consider the conditional probability that Xn = m given that the chain started at time 0 in state i and has not yet entered state r by time n, where r is a specified state not equal to either i or m. We are interested in whether this conditional probability is equal to the n stage transition probability of a Markov chain whose state space does not include state r and whose transition probabilities are

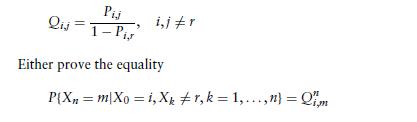
or construct a counterexample.

Pij Qij i,j r = 1-Pi Either prove the equality P(X=m\Xoi,Xkr, k = 1,...,n) = m