Question: 38. In Example 6.20, we computed m(t) = E[O(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain

38. In Example 6.20, we computed m(t) = E[O(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this quantity is by deriving a differential equation for it.

(a) Show that m(t + h) = m(t) + P00(t)h + o(h)

(b) Show that

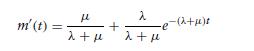
m' (t) = + e e-(x+1)8 +1 2+ u

(c) Solve for m(t).

m' (t) = + e e-(x+1)8 +1 2+ u

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Theory Of Probability Questions!

38. In Example 6.20, we computed m(t) = E[0(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this...

38. In Example 6.20, we computed m(t) = E[O(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this...

In Example 6.20, we computed m(t) = E[O(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this...

In Example 6.20, we computed m(t) =E[O(t)], the expected occupa- tion time in state 0 by time for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this...

Kindly assist me to solve the following Question 3 To estimate the population mean weight of out-going packages, a shipping company randomly samples 70 packages and finds a mean weight of 52 pounds....

In Example 6.24, we computed m(t) = E[O(t)], the expected occupation time in state 0 by time t for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this...

46. In Example 6.24, we computed , the expected occupation time in state 0 by time t for the two-state continuoustime Markov chain starting in state 0. Another way of obtaining this quantity is by...

Answer all please give eexplanations The mean number of customers appearing in a bank during a self-assertively picked hour is four. The bank boss is contemplating reducing the amount of tellers....

Supply Chain Management Introduction Outline What is supply chain management? Significance of supply chain management. Push vs. Pull processes utdallas.edu/~metin 1 A Generic Supply Chain Sources:...

Find and discuss business examples of overcapacity and under capacity.

X is the number of heads and Y the number of heads minus the number of tails obtained in three flips of a balanced coin, construct a table showing the values of the joint probability distribution of...

Your client is invested in a well - diversified portfolio of mutual funds. Recently he read about closed - end funds, and he wonders if he should consider adding them to his portfolio. As his...

Use the surface integral in Stokes Theorem to calculate the circulation of the field F around the curve C in the indicated direction. F = 2yi + 3xj - z 2 k C: The circle x 2 + y 2 = 9 in the...

Consider a set of n machines and a single repair facility to service these machines. Suppose that when machine i, i = 1,..., n, fails it requires an exponentially distributed amount of work with rate...

If (X()] and [Y(t)) are independent continuous-time Markov chains, both of which are time reversible, show that the process (X(t), Y(1)) is also a time reversible Markov chain.

Customers arrive at a service station, manned by a single server who serves at an exponential rate , at a Poisson rate A. After completion of service the customer then joins a second system where the...

Anderson Co. issued a $41,125, 60-day, discounted note to National Bank. The discount rate is 9%. At maturity, assuming a 360-day year, the borrower will pay a. $37,424 b. $41,125 c. $40,508 d....

5 Proctoring Enabled: The Co... 43 The ledger of Mai Company includes the following accounts with normal balances as of December 31: Common Stock $10,600; Dividends $1,600; Services Revenue $29,000;...

For each ratio, select the building block of financial statement analysis to which it best relates. 1. Return on total assets 2. Debt-to-equity ratio 3. Acid-test ratio 4. Times interest earned 5....